题目内容
如图,AB∥DC,∠B=55°,∠2=40°,∠3=85°.
(1)求∠D的度数;
(2)求∠1的度数;
(3)能否得到DA∥CB,请说明理由.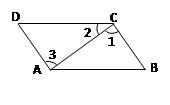
(1)求∠D的度数;
(2)求∠1的度数;
(3)能否得到DA∥CB,请说明理由.
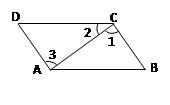
(1)在ACD中, ∵∠D+∠2+∠3=180°(三角形三个内角的和等于180°),
又∵∠2=40°,∠3=85°,
∴∠D=180°-40°-85°=55°.
(2)∵ AB∥DC, ∠=40°,
∴ ∠BAC=∠2=40°.
在ABC中, ∵∠BAC+∠1+∠B=180°(三角形三个内角的和等于180°),
又∵∠B=55°,
∴∠1=180°-40°-55°=85°.
(3)能得到DA∥CB. 理由如下:
∵∠1=85°, ∠3=85°,
∴∠3=∠1=85°.
∴ DA∥CB(内错角相等,两直线平行).
又∵∠2=40°,∠3=85°,
∴∠D=180°-40°-85°=55°.
(2)∵ AB∥DC, ∠=40°,
∴ ∠BAC=∠2=40°.
在ABC中, ∵∠BAC+∠1+∠B=180°(三角形三个内角的和等于180°),
又∵∠B=55°,
∴∠1=180°-40°-55°=85°.
(3)能得到DA∥CB. 理由如下:
∵∠1=85°, ∠3=85°,
∴∠3=∠1=85°.
∴ DA∥CB(内错角相等,两直线平行).
(1)∠D在△ADC中,另两个角度数已知,就可用三角形内角和定理求解.
(2)∠B,∠2已知,利用两直线平行同旁内角互补求解.
(3)等量代换后,再利用内错角相等,两直线平行判定.
(2)∠B,∠2已知,利用两直线平行同旁内角互补求解.
(3)等量代换后,再利用内错角相等,两直线平行判定.

练习册系列答案
相关题目





