题目内容
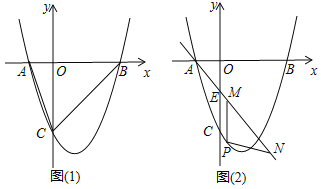
【题目】如图（1），抛物线
与x轴交于A（1，0）、B（t，0）（t >0）两点，与y轴交于点C（0，3），若抛物线的对称轴为直线x=1，
（1）求抛物线的函数解析式；
（2 若点D是抛物线BC段上的动点，且点D到直线BC的距离为
，求点D的坐标
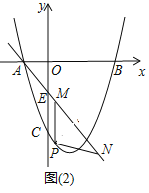
（3）如图（2），若直线y=mx+n经过点A，交y轴于点E（0，1），点P是直线AE下方抛物线上一点，过点P作x轴的垂线交直线AE于点M，点N在线段AM延长线上，且PM=PN，是否存在点P，使△PMN的周长有最大值？若存在，求出点P的坐标及△PMN的周长的最大值；若不存在，请说明理由．
【答案】（1）y=x22x3；（2）点D的坐标为（1，4）或（2，3）；（3）P点坐标为（
，
），△PMN的周长的最大值为
.
【解析】
(1)先根据对称轴和已知点A得出该点的对称点，再设出抛物线的表达式，将C点坐标再代入便可求得抛物线的解析式.
(2)设D点的坐标，根据三角形BCD的面积即可求出D点的坐标.
先根据A、E点求出直线y=mx+n,根据直线可知OA=OE,则∠OAE=∠OEA=45°,又根据MP∥EC,可知∠PMN=∠CEM=∠OEA=45°,又PM=PN,故△PMN是个等腰直角三角形，面积是（
）PM，设M点的坐标为（k，-k-1），则
，则当
时，PM的长有最大值
. 此时P点坐标为（，
），△PMN的周长的最大值为
（1）∵抛物线的对称轴为直线x=1，
则点A（1，0）关于直线x=1的对称点B的坐标为（3，0），
设抛物线的表达式为y=a（x3）（x+1），
将点C（0，3）代入上式得3a=-3，
解得：a=1，
∴抛物线的解析式为y=（x3）（x+1）=x22x3；
（2）∵点B（3，0）、C（0，-3），
则BC=3
，
∴S△BCD==
=3，
设D（x，x22x3），连接OD，
∴S△BCD=S△OCD+S△BODS△BOC
=3x+3（x2+2x+3）×3×3
=
=3
解得x=1或x=2
则点D的坐标为（1，4）或（2，3）
（3）设直线AE解析式为
，将点A（1，0）、E（0，1）代入，得
解得：
则直线AE解析式为
∵OA=OE=1，则∠OAE=∠OEA=45°，
又∵PM∥y轴，
∴∠PMN=∠CEN=∠AEO=45°
∵PM=PN
∴∠PMN=∠PNM =45°
∴
∴
设M（k，k1），P（k，
）
∴PM=
=
∴当k=时，PM的长有最大值为
∴P点坐标为（，），△PMN的周长的最大值为
