题目内容
【题目】已知二次函数y=（t+1）x2+2（t+2）x+ 
在x=0和x=2时的函数值相等．
（1）求二次函数的解析式；
（2）若一次函数y=kx+6的图象与二次函数的图象都经过点A（﹣3，m），求m和k的值；
（3）把二次函数的图象与x轴两个交点之间的部分记为图象G，把图象G向左平移n（n＞0）个单位后得到的图象记为M，请结合图象回答：当（2）中得到的直线与图象M有公共点时，求n的取值范围．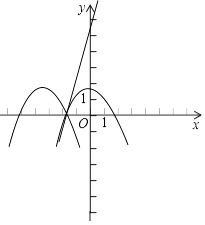
【答案】
（1）解：∵二次函数y=（t+1）x2+2（t+2）x+ 
在x=0和x=2时的函数值相等，
∴对称轴x=﹣ 
= 
=1，解得，t=﹣ ，
则二次函数的解析式为：y=（﹣ +1）x2+2（﹣ +2）x+ ，即y=﹣ 
（x+1）（x﹣3）或y=﹣ （x﹣1）2+2，
（2）解：∵二次函数的象经过点A（﹣3，m），
∴m=﹣ （﹣3+1）（﹣3﹣3）=﹣6．
又∵一次函数y=kx+6的图象经过点A（﹣3，m），；
∴m=﹣3k+6，即﹣6=﹣3k+6，
解得，k=4．
综上所述，m和k的值分别是﹣6、4；
（3）解：由题意可知，图象G的解析式是y=﹣ x2+x+ =﹣ （x2﹣2x﹣3）=﹣ （x﹣3）（x+1），﹣1≤x≤3，
则抛物线平移后得出的图象M的解析式是y=﹣ （x﹣3+n）（x+1+n），﹣n﹣1≤x≤3﹣n，
此时直线平的解析式是y=4x+6，
如果直线与平移后的二次函数相切，
则方程4x+6=﹣ （x﹣3+n）（x+1+n）有两个相等的实数解，
即x2+（2n+6）x+n2﹣6n+9=0有两个相等的实数解，。
判别式△=（2n+6）2﹣4×（n2﹣6n+9）=48n=0，
即n=0，
∵与已知n＞0相矛盾，
∴平移后的直线与平移后的抛物线不相切，
∴结合图象可知，如果平移后的直线与抛物线有公共点，
则两个临界的交点为（﹣n﹣1，0），（3﹣n，0），
则0=4（﹣n﹣1）+6，
n= ，
0=4（3﹣n）+6，
n= ，
即n的取值范围是： ≤n≤ ．
【解析】（1）根据已知条件知，该函数的对称轴方程为x=1，从而根据对称轴公式建立出关于t的方程,求出t的值，把t的值代入函数解析式即可，根据图像与坐标轴的交点坐标，顶点坐标画出图像；
（2）求出A点的坐标，再用待定系数法求出k的值；
（3）由题意可知，图象G的解析式是y=﹣ （x﹣3）（x+1），（﹣1≤x≤3，）得出抛物线平移后得出的图象M的解析式是y=﹣ （x﹣3+n）（x+1+n），（﹣n﹣1≤x≤3﹣n），此时直线平的解析式是y=4x+6，如两图像有一个交点时，得出方程方程4x+6=﹣ （x﹣3+n）（x+1+n）有两个相等的实数解，求出判别式△=（2n+6）2﹣4×（n2﹣6n+9）=48n=0，求出n的值与已知的值矛盾，得出平移后的直线与抛物线有两个公共点，设出两个临界的交点为（﹣n﹣1，0），（3﹣n，0），代入直线的解析式求出n的值，即可得出答案
