题目内容
如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A( ,﹣2),反比例函数y=
,﹣2),反比例函数y= (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l的解析式;
(2)在函数y= (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.

 ,﹣2),反比例函数y=
,﹣2),反比例函数y= (x>0)的图象过点A.
(x>0)的图象过点A.(1)求直线l的解析式;
(2)在函数y=
 (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(1)y= x﹣4;(2)(
x﹣4;(2)( ,﹣1).
,﹣1).
 x﹣4;(2)(
x﹣4;(2)( ,﹣1).
,﹣1).试题分析:(1)由A为直角三角形外心,得到A为斜边MN中点,根据A坐标确定出M与N坐标,设直线l解析式为y=mx+n,将M与N坐标代入求出m与n的值,即可确定出直线l解析式;
(2)将A坐标代入反比例解析式求出k的值,确定出反比例解析式,利用反比例函数k的意义求出△OBC的面积,由△ONP的面积是△OBC面积的3倍求出△ONP的面积,确定出P的横坐标,即可得出P坐标.
试题解析:(1)∵Rt△MON的外心为点A(
 ,﹣2),
,﹣2),∴A为MN中点,即M(3,0),N(0,﹣4),
设直线l解析式为y=mx+n,
将M与N代入得:
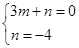 ,
,解得:m=
 ,n=﹣4,
,n=﹣4,则直线l解析式为y=
 x﹣4;
x﹣4;(2)将A(
 ,﹣2)代入反比例解析式得:k=﹣3,
,﹣2)代入反比例解析式得:k=﹣3,∴反比例解析式为y=﹣
 ,
,∵B为反比例函数图象上的点,且BC⊥x轴,
∴S△OBC=
 ,
,∵S△ONP=3S△OBC,
∴S△ONP=
 ,
,设P横坐标为a(a>0),
∴
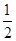 ON•a=3×
ON•a=3× ,即a=
,即a= ,
,则P坐标为(
 ,﹣1).
,﹣1).【考点】反比例函数综合题.

练习册系列答案
相关题目
 在第一象限内的图像与△ABC有交点,则
在第一象限内的图像与△ABC有交点,则 的取值范围是
的取值范围是


 的图象向左平移2个单位,再向下平移1个单位得到
的图象向左平移2个单位,再向下平移1个单位得到 的图象,则
的图象,则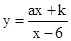 的图象经过B、E两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.
的图象经过B、E两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.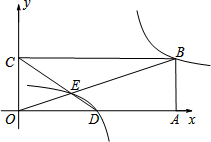
 (x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6).若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是 .
(x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6).若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是 .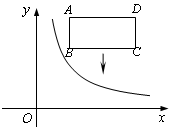
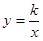 的图象经过点(﹣1,2),则k的值是
的图象经过点(﹣1,2),则k的值是  ,AE=
,AE=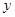 ,则能反映
,则能反映

 在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.
在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.