题目内容
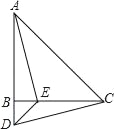
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠ACD的度数.
【答案】(1)证明见解析;(2)60°
【解析】试题分析:(1)利用SAS即可得证;
(2)由全等三角形对应角相等得到∠AEB=∠CDB,利用外角的性质求出∠AEB的度数,即可确定出∠BDC的度数,进而利用三角形的内角和得出∠ACD的度数.
试题解析:
(1)证明:在△ABE和△CBD中,
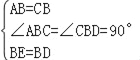 ,
,
∴△ABE≌△CBD(SAS);
(2)∵在△ABC中,AB=CB,∠ABC=90°,
∴∠BAC=∠ACB=45°,
由(1)得:△ABE≌△CBD,
∴∠AEB=∠BDC,
∵∠AEB为△AEC的外角,
∴∠AEB=∠ACB+∠CAE=30°+45°=75°,
∴∠BDC=75°.
∴∠ACD=180°﹣∠BAC﹣∠BDC=180°﹣45°﹣75°=60°.

练习册系列答案
相关题目
【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有![]() 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为![]() 元(利润=收入-支出).
元(利润=收入-支出).
(1)请写出![]() 与
与![]() 的关系式 ;
的关系式 ;
(2)完成表格.
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
|
|
|
|
|
|
| … |
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.