Question

【题目】在第九章中我们研究了几种特殊四边形，请根据你的研究经验来自己研究一种特殊四边形——筝形．

初识定义：两组邻边分别相等的四边形是筝形．

（1）根据筝形的定义，写出一种你学过的四边形满足筝形的定义的是 ．

性质研究：

（2）类比你学过的特殊四边形的性质，通过观察、测量、折叠、证明等操作活动，对如图的筝形ABCD（AB＝AD，BC＝CD）的性质进行探究，以下判断正确的有 （填序号）．

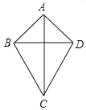
①AC⊥BD；②AC、BD互相平分；

③AC平分∠BAD和∠BCD；

④∠ABC＝∠ADC；⑤∠BAD＋∠BCD＝180°；

⑥筝形ABCD的面积为AC×BD．

（3）在上面的筝形性质中选择一个进行证明．

性质应用：

（4）直接利用你发现的筝形的性质解决下面的问题：

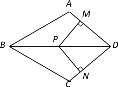
如图，在筝形ABCD中，AB＝BC，AD＝CD，点P是对角线BD上一点，过P分别做AD、CD垂线，垂足分别为点M、N．当筝形ABCD满足条件 时，四边形PNDM是正方形？请说明理由．

判定方法：

（5）回忆我们学习过的特殊四边形的判定方法（如四边相等的四边形是菱形），用文字语言写出筝形的一个判定方法（除定义外）： ．

Answer 1

【答案】（1）菱形（或正方形，答案不唯一）；（2）①③④⑥．（3）选①．证明见解析；（4）∠ADC＝90°． 证明见解析；（5）一条对角线垂直且平分另一条对角线的四边形是筝形．（答案不唯一，如一组邻边相等且对角线互相垂直的四边形是筝形等．）

【解析】

(1)根据筝形的定义，结合平行四边形、矩形、菱形、正方形的性质即可得；

(2)根据筝形的定义，结合线段垂直平分线的判定、全等三角形的判定与性质、四边形的面积进行分析即可得；

(3)根据筝形的定义，结合线段垂直平分线的判定、全等三角形的判定与性质、四边形的面积等选择任何一个性质进行证明即可；

(4)结合筝形的性质结合正方形的判定方法即可得；

(5)如：一条对角线垂直且平分另一条对角线的四边形是筝形．由AC是BD的垂直平分线，可得AB=AD，CB=CD．继而证得结论．(答案不唯一)

(1)由菱形和正方形的定义可知菱形(或正方形)是筝形，

故答案为：菱形(或正方形，答案不唯一)；

(2)∵四边形ABCD是筝形，AB＝AD，BC＝CD，

∴AC垂直平分BD，

∴AC⊥BD，故①正确，②错误；

∵AB＝AD，BC＝CD，AC＝AC，

∴△ABC≌△ADC，

∴∠BAC＝∠DAC，∠BCA＝∠DCA，∠ABC＝∠ADC，

∴AC平分∠BAD和∠BCD，故③、④正确，

∵AC⊥BD，

∴筝形ABCD的面积为AC×BD，故⑥正确，

无法推出⑤，故⑤错误，

故答案为：①③④⑥；

(3)选①，

证明：∵AB＝AD，BC＝CD，

∴AC垂直平分BD．

∴AC⊥BD．

答案不唯一，

选③，

证明：∵AB＝AD，BC＝CD，AC＝AC，

∴△ABC≌△ADC．

∴∠BAC＝∠DAC，∠BCA＝∠DCA．

∴AC平分∠BAD和∠BCD．

选④，

证明：∵AB＝AD，BC＝CD，AC＝AC，

∴△ABC≌△ADC．

∴∠ABC＝∠ADC．

选⑥，

证明：∵AB＝AD，BC＝CD，

∴AC垂直平分BD．

∴AC⊥BD．

∴筝形ABCD的面积为AC×BD．

(4)当筝形ABCD满足条件∠ADC＝90°时，四边形PNDM是正方形，理由如下：

∵PM⊥AD，PN⊥CD，

∴∠PMD＝∠PND＝90°．

又∵∠ADC＝90°，

∴四边形MPND是矩形．

∵在筝形ABCD中，AB＝BC，AD＝CD，

∴∠ADB＝∠CDB，

又∵PM⊥AD，PN⊥CD，

∴PM＝PN，

∴四边形MPND是正方形，

故答案为：∠ADC＝90°．

(5)一条对角线垂直且平分另一条对角线的四边形是筝形．(答案不唯一，如一组邻边

相等且对角线互相垂直的四边形是筝形等．)

已知：如图，在四边形ABCD中，AC是BD的垂直平分线．

求证：四边形ABCD是筝形．

证明：∵AC是BD的垂直平分线，

∴AB=AD，CB=CD，

∴四边形ABCD是筝形．