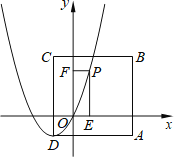
题目内容
【题目】如图,在正方形ABCD中,点A的坐标为(![]() ,
,![]() ),点D的坐标为(
),点D的坐标为(![]() ,
,![]() ),且AB∥y轴,AD∥x轴. 点P是抛物线
),且AB∥y轴,AD∥x轴. 点P是抛物线![]() 上一点,过点P作PE⊥x轴于点E,PF⊥y轴于点 F.
上一点,过点P作PE⊥x轴于点E,PF⊥y轴于点 F.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若点P在第二象限,当四边形PEOF是正方形时,求正方形PEOF的边长;
(3)以点E为顶点的抛物线![]() 经过点F,当点P在正方形ABCD内部(不包含边)时,求a的取值范围.
经过点F,当点P在正方形ABCD内部(不包含边)时,求a的取值范围.
【答案】(1)B (3,3);(2)正方形![]() 的边长为3;(3)
的边长为3;(3)![]() >3或
>3或![]() <
<![]() .
.
【解析】
(1)先利用A点和D点坐标得到正方形ABCD的边长为4,然后写出B点坐标;
(2)设点P(x,x2+2x),利用正方形的性质得到PE=PF,即x2+2x=-x,然后解方程求出x即可得到正方形PEOF的边长;
(3)设P(m,m2+2m)(m≠0),则E(m,0),F(0,m2+2m),利用顶点式表示以E为顶点的抛物线解析式为y=a(x-m)2,再把F(0,m2+2m)代入得m=![]() ,接着求出抛物线y=x2+2x与BC的交点坐标为(1,3),则利用点P在正方形ABCD内部(不包含边)得到-1<m<1且m≠0,然后分别解-1<
,接着求出抛物线y=x2+2x与BC的交点坐标为(1,3),则利用点P在正方形ABCD内部(不包含边)得到-1<m<1且m≠0,然后分别解-1<![]() <0和0<
<0和0<![]() <1即可.
<1即可.
(1)![]() (
(![]() ,
,![]() );(2)设点
);(2)设点![]() (
(![]() ,
,![]() ).
).
当四边形![]() 是正方形时,
是正方形时,![]() ,
,
当点![]() 在第二象限时,有
在第二象限时,有![]() .
.
解得![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴正方形![]() 的边长为
的边长为![]() .
.
(3)设点![]() (
(![]() ,
,![]() ),则点E(
),则点E(![]() ,
,![]() ),则点F(
),则点F(![]() ,
,![]() ).
).
∵![]() 为抛物线顶点,
为抛物线顶点,
∴该抛物线解析式为![]() .
.
∵抛物线经过点![]() ,
,
∴![]() ,化简得
,化简得![]() .
.
对于![]() ,令
,令![]() ,解得
,解得![]() ; 令
; 令![]() ,解得
,解得![]() .
.
∵点![]() 在正方形
在正方形![]() 内部,
内部,
∴![]() <
<![]() <
<![]() ,且
,且![]() .
.
①当![]() <
<![]() <
<![]() 时
时
由反比例函数性质知![]() ,∴
,∴![]() <
<![]() .
.
②当![]() <
<![]() <
<![]() 时
时
由反比例函数性质知![]() ,∴
,∴![]() >
>![]() .
.

练习册系列答案
相关题目