题目内容
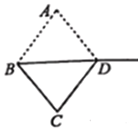
【题目】如图,菱形纸片ABCD中,![]() ,将纸片沿对角线BD剪开,再将
,将纸片沿对角线BD剪开,再将![]() 沿射线
沿射线![]() 的方向平移得到
的方向平移得到![]() .当
.当![]() 是直角三角形时,
是直角三角形时,![]() 平移的距离为___
平移的距离为___
【答案】![]() 或
或![]()
【解析】
根据菱形性质可求出OB=OD=3,OA=OC=4,设![]() 平移的距离为x,当∠A′D′C=90°时,利用勾股定理可得A′C2=x2+82=x2+64,A′D′2=25,D′C2=42+(3+x)2,
平移的距离为x,当∠A′D′C=90°时,利用勾股定理可得A′C2=x2+82=x2+64,A′D′2=25,D′C2=42+(3+x)2,
根据题意可得A′C2= A′D′2+ D′C2,列方程求出x值即可;同理当∠CA′D′=90°时,可得D′C2= A′C2+ A′D′2,列方程求出x值即可;综上即可得答案.
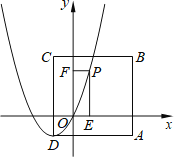
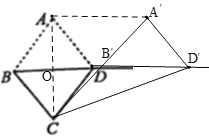
①如图,当∠A′D′C=90°时,连接AC,AA′,AC交BD于O,设![]() 平移的距离为x,
平移的距离为x,
∵AC、BD是菱形ABCD的对角线,
∴AC⊥BD,
∵AB=5,BD=6,
∴OB=OD=3,OA=OC=4,
∵将![]() 沿射线
沿射线![]() 的方向平移得到
的方向平移得到![]() ,
,
∴AA′=DD′=x,
∵AA′//BD,
∴∠CAA′=90°,
∴A′C2=x2+82=x2+64,A′D′2=25,D′C2=42+(3+x)2,
∵∠A′D′C=90°
∴A′C2= A′D′2+ D′C2,即x2+64=25+42+(3+x)2,
解得:x=![]() .
.

②如图,当∠CA′D′=90°时,
同①可得A′C2=x2+82=x2+64,A′D′2=25,D′C2=42+(3+x)2,
∵∠CA′D′=90°,
∴D′C2= A′C2+ A′D′2,即42+(3+x)2=x2+64+25,
解得:x=![]() ,
,
综上所述:![]() 平移的距离为
平移的距离为![]() 或
或![]() .
.

练习册系列答案
相关题目