题目内容
【题目】(10分)如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.
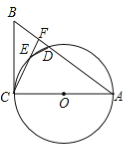
(1)若∠B+∠FED=90°,求证:BC是⊙O的切线;
(2)若FC=6,DE=3,FD=2,求⊙O的直径.
【答案】(1)详见解析;(2)⊙O的直径为9.
【解析】
试题分析: (1)由圆内接四边形对角互补可得∠A+∠DEC=180°,由邻补角的定义可得∠FED+∠DEC=180°,所以∠FED=∠A,又因∠B+∠FED=90°,即可得∠B+∠A=90°,所以∠BCA=90°,即BC是⊙O的切线;(2)由∠CFA=∠DFE,∠FED=∠A,即可得△FED∽△FAC,根据相似三角形的性质可得![]() ,带入数值即可求出AC的长.
,带入数值即可求出AC的长.
试题解析:(1)证明:∵∠A+∠DEC=180°,∠FED+∠DEC=180°,
∴∠FED=∠A,
∵∠B+∠FED=90°,
∴∠B+∠A=90°,
∴∠BCA=90°,
∴BC是⊙O的切线;
(2)解:∵∠CFA=∠DFE,∠FED=∠A,
∴△FED∽△FAC,
∴![]() ,
,
∴![]() ,
,
解得:AC=9,即⊙O的直径为9.

练习册系列答案
相关题目