题目内容
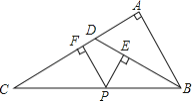
【题目】P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC= . 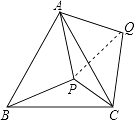
【答案】3:4:2
【解析】解:如图,将△APB绕A点逆时针旋转60°得△AQC,显然有△AQC≌△APB,连PQ, ∵AQ=AP,∠QAP=60°,
∴△AQP是等边三角形,
∴PQ=AP,
∵QC=PB,
∴△QCP的三边长分别为PA,PB,PC,
∵∠APB+∠BPC+∠CPA=360°,∠APB:∠BPC:∠CPA=5:6:7,
∴∠APB=100°,∠BPC=120°,∠CPA=140°,
∴∠PQC=∠AQC﹣∠AQP=∠APB﹣∠AQP=100°﹣60°=40°,
∠QPC=∠APC﹣∠APQ=140°﹣60°=80°,
∠PCQ=180°﹣(40°+80°)=60°,
∴∠PCQ:∠QPC:∠PQC=3:4:2,
所以答案是:3:4:2.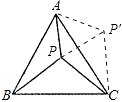
【考点精析】掌握等边三角形的性质和旋转的性质是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
相关题目