Question

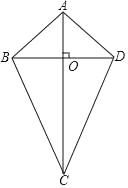
【题目】定义：一条对角线垂直平分另一条对角线的四边形叫做筝形，如图，筝形ABCD的对角线AC、BD相交于点O．且AC垂直平分BD．

（1）请结合图形，写出筝形两种不同类型的性质：性质1：　 　；性质2：　 　．

（2）若AB∥CD，求证：四边形ABCD为菱形．

Answer 1

【答案】（1）对角线互相垂直，是轴对称图形；（2）见解析

【解析】

（1）由筝形的定义即可得出结论；

（2）由垂直平分线的性质得出AB=AD，BO=DO，同理：BC=DC，由AS证明△AOB≌△CDO，得出AB=CD，因此AB=CD=BC=AD，即可得出四边形ABCD为菱形．

解：（1）由筝形的定义得：对角线互相垂直，即AC⊥BD；是轴对称图形，对称轴为AC；

故答案为：对角线互相垂直，是轴对称图形；

（2）∵AC垂直平分BD，

∴AB＝AD，BO＝DO，

同理：BC＝DC，

∵AB∥CD，

∴∠ABO＝∠ODC，

在△ABO和△CDO中，

，

∴△AOB≌△CDO（ASA），

∴AB＝CD，

∴AB＝CD＝BC＝AD，

∴四边形ABCD为菱形．