题目内容
【题目】已知A、B、C、D是⊙O上的四点, ![]() ,AC是四边形ABCD的对角线
,AC是四边形ABCD的对角线
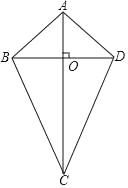
(1)如图1,连结BD,若∠CDB=60°,求证:AC是∠DAB的平分线;
(2)如图2,过点D作DE⊥AC,垂足为E,若AC=7,AB=5,求线段AE的长度.

【答案】(1)证明见解析;(2)1.
【解析】试题分析:(1)先根据![]() 可知
可知![]() 再由
再由![]() 可得出
可得出![]() 是等边三角形,故
是等边三角形,故![]() 由圆周角定理即可得出结论;
由圆周角定理即可得出结论;
(2)首先连接![]() ,在线段
,在线段![]() 上取点
上取点![]() ,使得
,使得![]() 连接
连接![]() ,易证得
,易证得![]() 继而可求得线段
继而可求得线段![]() 的长度.
的长度.
试题解析:(1)证明: ![]()
![]()
![]()
∴△BCD是等边三角形,
![]()
∴∠CAD=∠BAC,即AC是∠DAB的平分线;
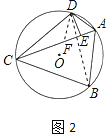
(2)连接BD,在线段CE上取点F,使得EF=AE,连接DF,
∵DE⊥AC,
∴DF=DA,
∴∠DFE=∠DAE,
![]()
∴CD=BD,∠DAC=∠DCB,
∴∠DFE=∠DCB,
∵四边形ABCD是圆的内接四边形,
![]()
![]()
∴∠DFC=∠DAB,
∵在△CDF和△BDA中,
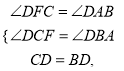
![]()
∴CF=AB=5,
∵AC=7,AB=5,
![]()

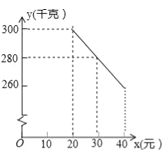
【题目】某电器超市销售每台进价分别为160元,200元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入/元 | |
A种型号/台 | B种型号/台 | ||
第1周 | 3 | 5 | 1800 |
第2周 | 4 | 10 | 3200 |
(1)A、B两种型号的电风扇的销售单价是多少?
(2)若该超市准备用不多于5400元的金额再次采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
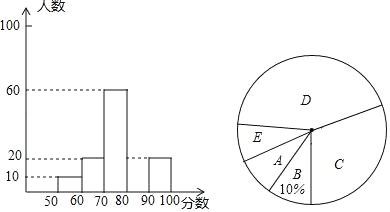
【题目】2018“体彩杯”重庆开州汉丰湖半程马拉松赛开跑前一周,某校七年级数学研究学习小组在某十字路口随机调查部分市民对“半马拉松赛”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
A | 50<n≤60 |
B | 60<n≤70 |
C | 70<n≤80 |
D | 80<n≤90 |
E | 90<n≤100 |
(1)本次调查的总人数为 人,在扇形统计图中“C”所在扇形的圆心角的度数为 度;
(2)补全频数分布图;
(3)若在这一周里,该路口共有7000人通过,请估计得分超过80的大约有多少人?