题目内容
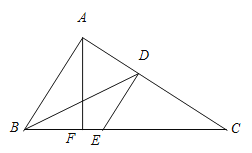
【题目】如图,矩形ABCD中,AB=6,BC=8,E为AB上一点,且AE=2,M为AD上一动点(不与A、D重合),AM=x,连结EM并延长交CD的延长线于F,过M作MG⊥EF交直线BC于点G,连结EG、FG.

(1)如图1,若M是AD的中点,求证:①△AEM≌△DFM;②△EFG是等腰三角形;
(2)如图2,当x为何值时,点G与点C重合?
(3)当x=3时,求△EFG的面积.
【答案】(1)证明见解析(2)当x=2或6时,点G与点C重合(3)![]()
【解析】试题分析:(1)①根据已知条件,利用ASA即可证得△AEM≌△DFM;②由△AEM≌△DFM可得EM=FM,又因MG⊥EF,根据线段垂直平分线的性质即可得EG=FG,结论得证;(2)当点G与点C重合时,易证△AEM∽△DMC,根据相似三角形的对应边成比例即可求得x值;(3)过G作GN⊥AD于N(如图3所示),证明△AEM∽△NMG,根据相似三角形的性质可求得MN=2AE=4,利用勾股定理求得EM的长,再证明△DMF∽△NGM,根据相似三角形的性质求得FM的长,进而的EF的长,根据△EFG的面积=![]() EFGM即可得结论.
EFGM即可得结论.
试题解析:
(1)证明:①∵四边形ABCD是矩形,
∴∠A=∠ADC=∠MDF=90°,
∵M是AD的中点,
∴AM=DM,
在△AEM和△DFM中,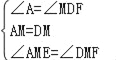 ,
,
∴△AEM≌△DFM(ASA);
②∵△AEM≌△DFM,
∴EM=FM,
又∵MG⊥EF,
∴EG=FG,
∴△EFG是等腰三角形;
(2)解:当点G与点C重合时,
∵∠A=∠EMC=∠ADC=90°,
∴∠AME+∠CMD=∠CMD+∠DCM,
∴∠AME=∠DCM,
∴△AEM∽△DMC,
∴![]() ,
,
∴![]() ,
,
解得:x1=2,x2=6,
∴当x=2或6时,点G与点C重合;
(3)解:过G作GN⊥AD于N,如图3所示:
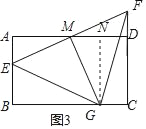
∴∠A=∠GNM=90°,GN=CD=6,
∴∠AME+∠NMG=∠NMG+∠NGM=90°,
∴∠AME=∠MGN,
∴△AEM∽△NMG,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
∴MN=2AE=4,
由勾股定理得:EM=![]() =
=![]() =
=![]() ,
,
∴GM=2EM=2![]() ,
,
∵AB∥CD,
∴△DMF∽△NGM,
∴![]() =
=![]() ,
,
解得:MF=![]() ,
,
∴EF=EM+MF=![]() ,
,
∴△EFG的面积=![]() EFGM=
EFGM=![]() .
.

 阅读快车系列答案
阅读快车系列答案