题目内容
【题目】在△ABC中,如图∠BAC=90°,BD平分∠ABC,点E在BC上,DE∥AB,点F在BC上,连结AF,∠C=36°.
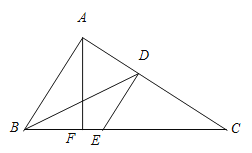
(1)求∠BDE的度数;
(2)若∠BAF∶∠CAF=2∶3,求证:AF⊥BC.
【答案】(1)27°;(2)见解析.
【解析】
(1)由∠BAC=90°和∠C=36°,可求得∠ABC,由BD平分∠ABC得∠ABD=![]() ∠ABC,
∠ABC,
再由DE∥AB,根据两直线平行,内错角相等可得∠BDE=∠ABD,问题得解;
(2)由∠BAF∶∠CAF=2∶3,可计算出∠CAF的度数,验证它与∠C的和等于90°即可.
(1)解:∵∠BAC=90°,∠C=36°,
∴∠ABC=54°,
∵BD平分∠ABC,
∴∠ABD=![]() ∠ABC=27°,
∠ABC=27°,
∵DE∥AB,
∴∠BDE=∠ABD=27°;
(2)证明:∵∠BAF∶∠CAF=2∶3,
∴∠CAF=![]() ∠BAC=
∠BAC=![]() ×90°=54°,
×90°=54°,
∵∠C=36°,
∴∠CAF+∠C=54°+36°=90°,
即∠AFC=90°,
∴AF⊥BC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




