��Ŀ����
����Ŀ��ͼ1��ͼ2��������״�ʹ�С��ȫ��ͬ�ķ���ֽ������ֽ��ÿ��С�����εı߳���Ϊ1���߶�AB�������˵����С�����εĶ����ϣ�

��1����ͼ1����С�����εĶ�����ȷ��һ��C������AC��BC��ʹ�á�ABCΪֱ�������Σ������Ϊ5����ֱ��д����ABC���ܳ���
��2����ͼ2����С�����εĶ�����ȷ��һ��D������AD��BD��ʹ�á�ABD����һ���ڽ�Ϊ45���������Ϊ3��
���𰸡���1��5+3![]() ;��2��3.
;��2��3.
�������������������1������ֱ�������Σ�AB=![]() ����ֱ�DZ�,�����5�������������һ��ֱ�DZ�BC���ȣ��������AC.
����ֱ�DZ�,�����5�������������һ��ֱ�DZ�BC���ȣ��������AC.
(2)�ȹ���һ��45��ǣ������������3���ɻ���ͼ��.
���������
��1���⣺��ͼ1��ʾ����ABC��Ϊ����
��ABC���ܳ�Ϊ�� ![]() +2
+2![]() +5=5+3
+5=5+3![]() ��
��

��2���⣺��ͼ2��ʾ����ABD�У���ADB=45���������Ϊ3��

�����͡������
��������
23
����Ŀ��Ϊ�˽������������������������������������ѧ�����ˡ�վ�ˡ����˵ĺû���������һ��ѧ����һ�����ϲ������ƣ�������ͻ����һ�������أ�������ͳ�ƽ������������������������ͳ��ͼ�������ͼ��������Ϣ����������⣺

��1������α�������������ѧ��һ���ж����ˣ�
��2�����ڱ������ѧ�����������õ�ѧ����������������ͳ��ͼ����������
��3����ȫ����5��������������ô����ȫ�г������У����˺�վ�˲�����ѧ�����ж����ˣ�
���𰸡���1��500������2��75������3��2.5��
�������������������1������������������ռ�ٷֱȾ���������.(2)������������15%.
(3) ���˺�վ�˲�����ѧ����ѧ���İٷֱȳ���������.
���������
��1���⣺100��20%=500��������
����α�������������ѧ��һ����500����
��2���⣺�������õ�ѧ��������500��15%=75����
��ȫͳ��ͼ��ͼ��ʾ��
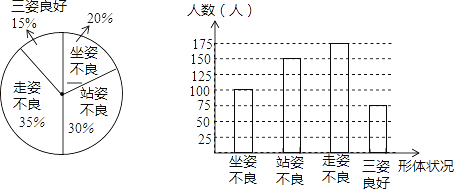
��3���⣺5������20%+30%��=2.5��
��ȫ�г������У����˺�վ�˲�����ѧ����2.5���ˣ�

����Ŀ����ͼ���۲�ÿ�����������![]() �ı仯���������������⣺
�ı仯���������������⣺
 ����
����
(1)������ı���������
������εı��� | 3 | 4 | 5 | 6 | ���� |
|
| _________ | _________ | _________ | _________ | ���� | _________ |
(2)���ݹ��ɣ��Ƿ����һ����![]() ���Σ�ʹ���е�
���Σ�ʹ���е�![]() �������ڣ�д��
�������ڣ�д��![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
(3)���ݹ��ɣ��Ƿ����һ����![]() ���Σ�ʹ���е�
���Σ�ʹ���е�![]() �������ڣ�д��
�������ڣ�д��![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.





