Question

【题目】如图，在Rt△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，动点M以每秒1cm的速度从点B向点C移动；同时动点N以3cm的速度从点C向A移动，当点N到达点A时，两点都停止移动，连接MN，设移动时间为t秒．

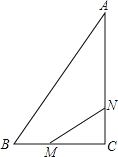
（1）当t为何值时，S△MNC＝S四边形ABMN？

（2）当t为何值时，△MNC与△ABC相似？

Answer 1

【答案】（1）t＝2；（2）t为或

【解析】

（1）由题意可知：CM＝6﹣t，CN＝3t，因为S△MNC＝S四边形ABMN，所以S△MNC是△ABC的面积一半，由此列出方程解答即可；

（2）分两种情况：△MCN∽△ACB，△MCN∽△BCA，得出对应线段的比计算得出答案即可．

解：（1）∵AC＝8cm，BC＝6cm，

∴S△ABC＝24cm2，

∵CM＝6﹣t，CN＝3t，S△MNC＝S四边形ABMN，

∴×3t（6﹣t）＝12，

解得：t1＝2，t2＝4；

∵当点N到达点A时，两点都停止移动，

∴0＜t＜，

∴当t＝2时，S△MNC＝S四边形ABMN．

（2）①当△MCN∽△ACB时，

则＝，

即＝，

解得：t＝；

②当△MCN∽△BCA时，

则＝，

即＝，

解得：t＝，

答：当t为或时，△MNC与△ABC相似．