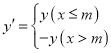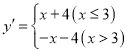��Ŀ����
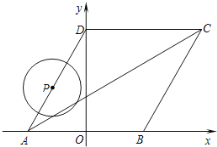
����Ŀ����ƽ��ֱ������ϵxOy�У���P��Q�������ԭ��Գƣ���Ƶ�P���Q��һ������г���������ʾΪ[P��Q]������[P��1��2����Q����1����2��]��һ������г�������
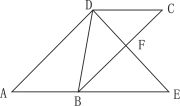
��1��д������������y��![]() ͼ���ϵ�һ������г�������
ͼ���ϵ�һ������г�������
��2����֪���κ���y��x2+mx+n��
�����˺���ͼ���ϴ���һ����г���[A��B]�����е�A������Ϊ��2��4������m��n��ֵ��
���ڢٵ������£���y����ȡһ��M��0��b��������AMBΪ���ʱ����b��ȡֵ��Χ��
���𰸡���1����ȡ[P��1��1����Q����1����1��]����2����m=2,n=-4����b��ȡֵ��ΧΪ![]() ��
��![]() ��
��
��������
��1������Ŀ��������г��ԵĶ����֪P��Q��Ϊ����ԭ��ԳƵ������㣬�ڷ���������ͼ�����ҳ����㼴�ɣ�
��2������A��BΪ��г��Կ���õ�B�����꣬��ɵõ�����m��n�ķ����飬�������ֵ���ڵ�M��x���Ϸ�ʱ��������á�AMBΪֱ��ʱ��Ӧ��M������꣬����M�����˶�ʱ�����AMBΪ��ǣ�����M��x���·�ʱ��ͬ�������b��ȡֵ��Χ��
�⣺��1����y��![]() ��
��
���ȡ[P��1��1����Q����1����1��]��
��2���١�A��2��4����A��BΪ��г��ԣ�
��B����������2����4����
��A��B�����������y��x2+mx+n���ɵ�![]() ��
��
��![]() ��
��
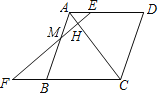
����ͼ��
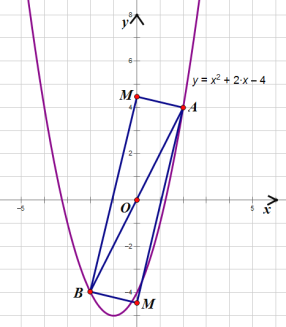
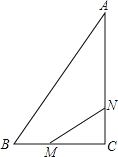
������ M����x���Ϸ�ʱ��
����AMB Ϊֱ�ǣ�M����x���ϣ�������ABCΪֱ�������Σ�
��A��2��4����A��BΪ��г��ԣ�B������Ϊ����2����4����
��ԭ��O��AB�߶�����OΪAB�е㣬
��AB��2OA��
��A��2��4����
��OA��![]() ��
��
��AB��![]() ��
��
��Rt��ABC��
��OΪAB�е�
��MO��OA��![]() ��
��
����AMB Ϊ��ǣ���![]() ��
��
������ M����x���·�ʱ��ͬ���ɵã� ![]() ��
��
����������b��ȡֵ��ΧΪ��![]() ��
��![]() ��
��

����Ŀ�����κ���y��ax2+bx+c��a��0���е�x��y�IJ��ֶ�Ӧֵ���±���
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 | �� |
y | �� | 12 | 5 | 0 | ��3 | ��4 | ��3 | 0 | 5 | �� |
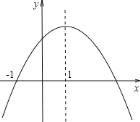
�������½��ۣ���1�����κ���y��ax2+bx+c����Сֵ����СֵΪ��3����2������![]() ��x��2ʱ��y��0����3����֪��A��x1��y1����B��x2��y2���ں�����ͼ���ϣ���1��x1��0��3��x2��4ʱ��y1��y2��������������ȷ�Ľ��۸���Ϊ��������
��x��2ʱ��y��0����3����֪��A��x1��y1����B��x2��y2���ں�����ͼ���ϣ���1��x1��0��3��x2��4ʱ��y1��y2��������������ȷ�Ľ��۸���Ϊ��������
A.0B.1C.2D.3