Question

【题目】抛物线y＝ax2﹣2ax﹣3a图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于C点，顶点M的纵坐标为4，直线MD⊥x轴于点D．

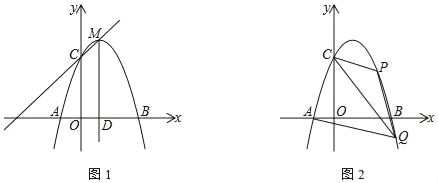
（1）求抛物线的解析式；

（2）如图1，N为线段MD上一个动点，以N为等腰三角形顶角顶点，NA为腰构造等腰△NAG，且G点落在直线CM上．若在直线CM上满足条件的G点有且只有一个时，请直接写出点N的坐标．

（3）如图，点P为第一象限内抛物线上的一点，点Q为第四象限内抛物线上一点，点Q的横坐标比点P的横坐标大1，连接PC、AQ．当PC＝AQ时，求S△PCQ的值．

Answer 1

【答案】（1）y＝﹣x2+2x+3；（2）点N的坐标为（1，﹣4+2 ）或（1，3）；（3）

【解析】

（1）求出对称轴得到顶点坐标，代入解析式求出a值即可．
（2）当直线CM上满足条件的G点有且只有一个时，可分两种情况讨论：①NG⊥CM，且NG=NA，如图2，作CH⊥MD于H，如图2．设N（1，n），易得NG=MN=（4-n），NA2=22+n2=4+n2，由题可得NG=NA，由此即可得到关于n的方程，解这个方程就可解决问题；②A、N、G共线，且AN=GN，如图3，过点GT⊥x轴于T，则有AD=DT=2，运用待定系数法求出直线CM的解析式，从而得出点G的坐标，然后运用三角形的中位线定理就可解决问题．
（3）根据点P在第一象限，点Q在第二象限，且横坐标相差1，进而设出点P（3-m，-m2+4m）（0＜m＜1）；得出点Q（4-m，-m2+6m-5），得出CP2，AQ2，最后建立方程求解即可．

解：（1）将顶点M坐标（1，4）代入解析式，可得a＝﹣1，抛物线解析式为y＝﹣x2+2x+3

（2）当直线CM上满足条件的G点有且只有一个时，

①NG⊥CM，且NG＝NA，如图1，

作CH⊥MD于H，

则有∠MGN＝∠MHC＝90°．

设N（1，n），

当x＝0时，y＝3，点C（0，3）．

∵M（1，4），

∴CH＝MH＝1，

∴∠CMH＝∠MCH＝45°，

∴NG＝MN＝（4﹣n）．

在Rt△NAD中，

∵AD＝DB＝2，DN＝n，

∴NA2＝22+n2＝4+n2．

则（4﹣n）2＝4+n2

整理得：n2+8n﹣8＝0，

解得：n1＝﹣4+2，n2＝﹣4﹣2（舍负），

∴N（1，﹣4+2）．

②A、N、G共线，且AN＝GN，如图2．

过点GT⊥x轴于T，

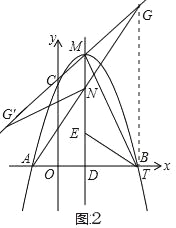
则有DN∥GT，

根据平行线分线段成比例可得AD＝DT＝2，

∴OT＝3．

设过点C（0，3）、M（1，4）的解析式为y＝px+q，

则，解得，

∴直线CM的解析式为y＝x+3．

当x＝3时，y＝6，

∴G（3，6），GT＝6．

∵AN＝NG，AD＝DT，

∴ND＝GT＝3，

∴点N的坐标为（1，3）．

综上所述：点N的坐标为（1，﹣4+2 ）或（1，3）．

（3）如图3，过点P作PD⊥x轴交CQ于D，

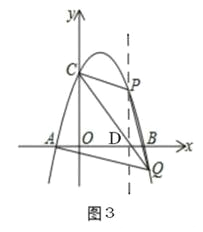
设P（3﹣m，﹣m2+4m）（0＜m＜1）；∵C（0，3），

∴PC2＝（3﹣m）2+（﹣m2+4m﹣3）2＝（m﹣3）2[（m﹣1）2+1]，

∵点Q的横坐标比点P的横坐标大1，

∴Q（4﹣m，﹣m2+6m﹣5），

∵A（﹣1，0）．

∴AQ2＝（4﹣m+1）2+（﹣m2+6m﹣5）2＝（m﹣5）2[（m﹣1）2+1]

∵PC＝AQ，

∴81PC2＝25AQ2，

∴81（m﹣3）2[（m﹣1）2+1]＝25（m﹣5）2[（m﹣1）2+1]，

∵0＜m＜1，

∴[（m﹣1）2+1]≠0，

∴81（m﹣3）2＝25（m﹣5）2，

∴9（m﹣3）＝±5（m﹣5），

∴m＝或m＝（舍），

∴P（，），Q（，﹣），

∵C（0，3），

∴直线CQ的解析式为y＝﹣x+3，

∵P（，），

∴D（，），

∴PD＝+＝

∴S△PCQ＝S△PCD+S△PQD＝PD×xP+PD×（xQ﹣xP）＝PD×xQ＝＝．