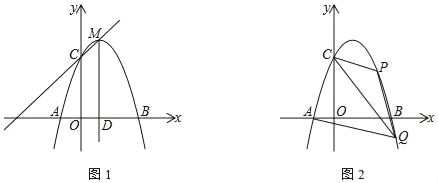题目内容
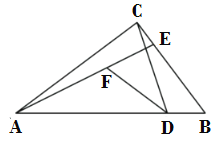
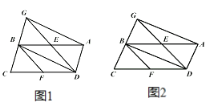
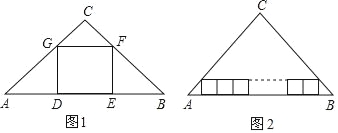
【题目】在△ABC中,∠C=90°,AC=4,BC=3,如图1,四边形DEFG为△ABC的内接正方形,则正方形DEFG的边长为_____.如图2,若三角形ABC内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为_____.
【答案】![]() ;
; ![]()
【解析】
(1)根据题意画出图形,作CN⊥AB,再根据GF∥AB,可知△CGF∽△CAB,由相似三角形的性质即可求出正方形的边长;
(2)①作CN⊥AB,交GF于点M,交AB于点N,同(1)可知,△CGF∽△CAB,根据对应边的比等于相似比可求出正方形的边长;
②方法与①类似;③作CN⊥AB,交GF于点M,交AB于点N,同(1)可知,△CGF∽△CAB,根据对应边的比等于相似比可求出正方形的边长;
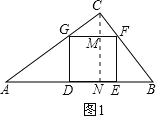
解:(1)在图1中,作CN⊥AB,交GF于点M,交AB于点N.
在Rt△ABC中,
∵AC=4,BC=3,∴AB=5,
∴![]() ABCN=
ABCN=![]() BCAC,∴CN=
BCAC,∴CN=![]() ,
,
∵GF∥AB, ∴△CGF∽△CAB,
∴CM:CN=GF:AB,
设正方形边长为x,
则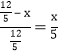 ∴x=
∴x= ![]() ;
;
故答案为:![]()
(2)①在图2中,作CN⊥AB,交GF于点M,交AB于点N.
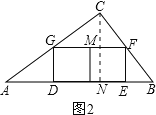
∵GF∥AB, ∴△CGF∽△CAB,
∴CM:CN=GF:AB,
设每个正方形边长为x,则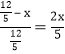
∴x=![]() .
.
②类比①,在图3中,
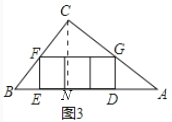
∵△CGF∽△CAB,
∴CM:CN=GF:AB,
设每个正方形边长为x,则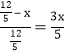
∴x=![]() .
.
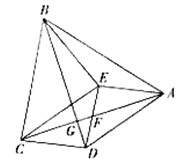
③在图4中,过点C作CN⊥AB,垂足为N,交GF于点M,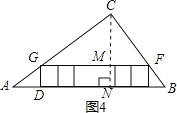
∵△CGF∽△CAB,
∴CM:CN=GF:AB,
设每个正方形边长为x,则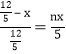 ,
,
∴=![]() .
.
故答案为:![]()

【题目】某班“数学兴趣小组”对函数![]() ,的图象和性质进行了探究过程如下,请补充完成:
,的图象和性质进行了探究过程如下,请补充完成:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________________;
的取值范围是__________________;
(2)下表是![]() 与
与![]() 的几组对应值.请直接写出
的几组对应值.请直接写出![]() ,
,![]() 的值:
的值:![]() ______________;
______________;![]() ________.
________.
| … |
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| -3 | 5 | 3 |
|
| … |
(3)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
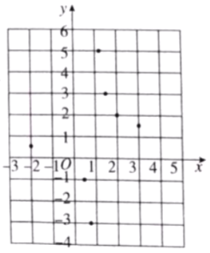
(4)通过观察函数的图象,小明发现该函数图象与反比例函数![]() 的图象形状相同,是中心对称图形,且点
的图象形状相同,是中心对称图形,且点![]() 和
和![]() 是一组对称点,则其对称中心的坐标为________.
是一组对称点,则其对称中心的坐标为________.
(5)请写出一条该函数的性质:___________________.
(6)当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有实数解,求
有实数解,求![]() 的取值范围.
的取值范围.
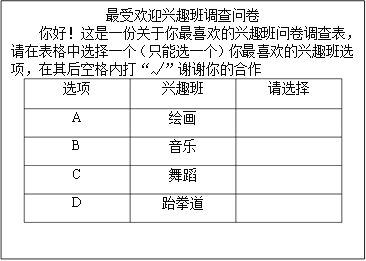
【题目】某市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班,为了解学生对这四类兴趣班的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表
兴趣班 | 频数 | 频率 |
A | 0.35 | |
B | 18 | 0.30 |
C | 15 |
|
D | 6 | |
合计 |
| 1 |
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)根据调查结果,请你估计该市2000名小学生中最喜欢“绘画”兴趣的人数;
(3)王姝和李要选择参加兴趣班,若他们每人从![]() 、
、![]() 、
、![]() 、
、![]() 四类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类的概率.
四类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类的概率.