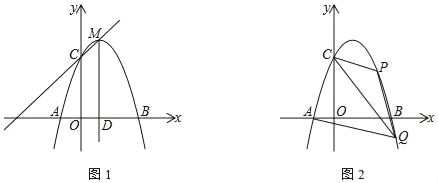题目内容
【题目】在平面直角坐标系中,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的交点
轴的交点![]() 与
与![]() 轴交于点
轴交于点![]() .
.
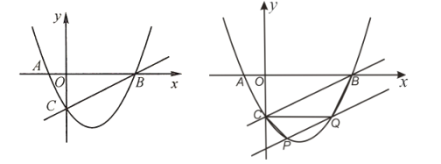
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方抛物线上的一点,过点
下方抛物线上的一点,过点![]() 作
作![]() 的平行线交抛物线于点
的平行线交抛物线于点![]() (点
(点![]() 在点
在点![]() 右侧),连结
右侧),连结![]() 、
、![]() ,当
,当![]() 的面积为
的面积为![]() 面积的一半时,求
面积的一半时,求![]() 点的坐标;
点的坐标;
(3)现将该抛物线沿射线![]() 的方向进行平移,平移后的抛物线与直线
的方向进行平移,平移后的抛物线与直线![]() 的交点为
的交点为![]() 、
、![]() (点
(点![]() 在点
在点![]() 的下方),与
的下方),与![]() 轴的右侧交点为
轴的右侧交点为![]() ,当
,当![]() 与
与![]() 相似,求出点
相似,求出点![]() 的横坐标.
的横坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由对称性求得点![]() ,待定系数即可求得二次函数解析式;
,待定系数即可求得二次函数解析式;
(2)由题可知![]() ,设出直线
,设出直线![]() 的方程,联立二次函数的解析式,由韦达定理即可容易求得.
的方程,联立二次函数的解析式,由韦达定理即可容易求得.
(3)由平移的性质,结合![]() ,求得
,求得![]() 的方程组,求解即可.
的方程组,求解即可.
解:(1)由对称性可知![]() ,
,
设抛物线解析式为![]() ,
,
代入![]() ,得
,得![]() ,
,
∴![]() ;
;
(2)由平行线间距离处处相等可知,
当![]() 的面积为
的面积为![]() 面积的一半时,
面积的一半时,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
即![]() ,
,
∵直线![]() 的解析式为
的解析式为![]() ,
,![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,![]() ,
,
联立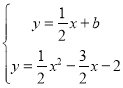 ,得
,得![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]()
(3)由![]() ,
,![]() ,得直线
,得直线![]() 的解析式为
的解析式为![]() ,
,
设点![]() 坐标为
坐标为![]() ,由平移的性质可知:
,由平移的性质可知:![]() ,
,
平移距离为![]() ,∴
,∴![]() ,
,
当![]() 与
与![]() 相似,只有
相似,只有![]() ,
,
∴![]() ,
,
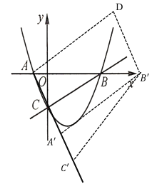
过点![]() 作
作![]() 的平行线,交原抛物线于点
的平行线,交原抛物线于点![]() ,连结
,连结![]() ,
,
四边形![]() 为平行四边形,点
为平行四边形,点![]() 的纵坐标为
的纵坐标为![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,则点
,则点![]() 坐标
坐标![]() ,
,
∴![]() ,①
,①
将点![]() 代入
代入![]() ,得:
,得:
![]() ,②
,②
联立方程①②,解得:![]() ,
,
![]() ,
,![]() (舍去负值),
(舍去负值),
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目