题目内容
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),先将△ABC沿一确定方向平移得到△A![]() B
B![]() C
C![]() ,点B的对应点B
,点B的对应点B![]() 的坐标是(1,2),再将△A
的坐标是(1,2),再将△A![]() B
B![]() C
C![]() 绕原点O顺时针旋转90°得到△A
绕原点O顺时针旋转90°得到△A![]() B
B![]() C
C![]() ,点A
,点A![]() 的对应点为点A
的对应点为点A![]() .
.
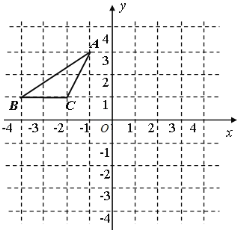
(1) 画出△A![]() B
B![]() C
C![]() ;
; ![]()
(2) 画出△A![]() B
B![]() C
C![]() ;
;
(3) 求出在这两次变换过程中,点A经过点A![]() 到达点A
到达点A![]() 的路径总长.
的路径总长.
【答案】(1)作图见解析;(2)作图见解析;(3)![]() .
.
【解析】
(1)由B点坐标和B1的坐标得到△ABC向右平移5个单位,再向上平移1个单位得到△A1B1C1,则根据点平移的规律写出A1和C1的坐标,然后描点即可得到△A1B1C1;
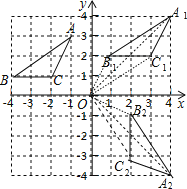
(2)利用网格特点和旋转的性质画出点A1的对应点为点A2,点B1的对应点为点B2,点C1的对应点为点C2,从而得到△A2B2C2;
(3)先利用勾股定理计算平移的距离,再计算以OA1为半径,圆心角为90°的弧长,然后把它们相加即可得到这两次变换过程中,点A经过点A1到达A2的路径总长.
(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)OA1=![]() ,
,
点A经过点A1到达A2的路径总长=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某商店代销一批季节性服装,每套代销成本40元,第一个月每套销售定价为52元时,可售出180套;应市场变化调整第一个月的销售价,预计销售定价每增加1元,销售量将减少10套。
(1)若设第二个月的销售定价每套增加x元,填写下表。
时间 | 第一个月 | 第二个月 |
每套销售定价(元) | ||
销售量(套) |
(2)若商店预计要在这两个月的代销中获利4160元,则第二个月销售定价每套多少元?
【题目】一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
A | B | C | D | E | 平均分 | 方差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| 2 |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
|
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?