Question

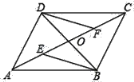
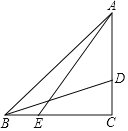
【题目】如图，△ABC中，∠C＝90°，AC＝BC，D、E分别在AC、BC上，若∠DBC＝2∠BAE，AB＝4，CD＝，则CE的长为_____．

Answer 1

【答案】2

【解析】

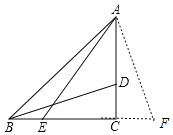
如图，延长BC至F，使CF＝CD＝，连接AF，由等腰直角三角形的性质可得AC＝BC＝4，∠ABC＝∠BAC＝45°，由勾股定理可求AF＝，由“SAS”可证△ACF≌△BCD，可得∠CAF＝∠CBD＝2α，可求∠EAF＝45°﹣α+2α＝45°+α＝∠AEF，可得AF＝EF，即可求解．

解：如图，延长BC至F，使CF＝CD＝，连接AF，

∵∠C＝90°，AC＝BC，AB＝4，

∴AC＝BC＝4，∠ABC＝∠BAC＝45°，

∴AF＝,

设∠BAE＝α，则∠DBC＝2α，

∴∠AEF＝∠ABC+∠BAE＝45°+α，∠EAC＝45°﹣α

∵BC＝AC，∠BCD＝∠ACF＝90°，CD＝CF，

∴△ACF≌△BCD（SAS）

∴∠CAF＝∠CBD＝2α，

∴∠EAF＝45°﹣α+2α＝45°+α＝∠AEF，

∴AF＝EF＝，

∴EC＝EF﹣CF＝，

故答案为：2．