Question

【题目】（1）解方程：；

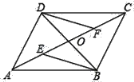
（2）如图，四边形ABCD的对角线AC、BD交于点O，已知O是AC的中点，AE=CF，DE∥BE，求证：△BOE≌△DOF．

Answer 1

【答案】（1）x=；（2）详见解析.

【解析】

（1）两边都乘以2x（x+1）化分式方程为整式方程，解之求得x的值，检验后即可；
（2）由DF与BE平行，得到内错角相等，再由O为AC的中点，得到OA=OC，又AE=CF，得到OE=OF，利用AAS即可得证．

解：（1）去分母，得：3（x+1）=8x，

解得：x=，

检验：当x=时，2x（x+1）=≠0

∴原方程的根是x=；

（2）∵O是AC的中点，

∴OA=OC，

∵AE=CF，

∴OA﹣AE=OC﹣CF，即OE=OF，

∵DF∥BE，

∴∠OBE=∠ODF，

在△BOE和△DOF中，

∵ ,

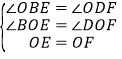∴△BOE△DOF（AAS）．