��Ŀ����
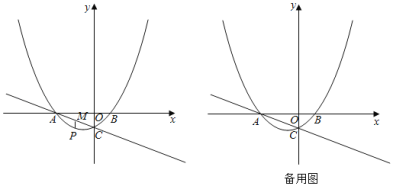
����Ŀ����ͼ��������![]() ��x����A��B���㣬��y���ڵ�C��ֱ��
��x����A��B���㣬��y���ڵ�C��ֱ��![]() ������A��C��
������A��C��
��1���������ߵĽ���ʽ��
��2����P����������һ���㣬����P��x��Ĵ��ߣ���ֱ��AC�ڵ�M�����P�ĺ�����Ϊm��
�ٵ�![]() ��ֱ��������ʱ�����P�����ꣻ
��ֱ��������ʱ�����P�����ꣻ
������B���ڵ�C�ĶԳƵ�![]() ����ƽ���ڴ���ֱ��l��ʹ��M��B��
����ƽ���ڴ���ֱ��l��ʹ��M��B��![]() ����ֱ�ߵľ��붼��ȣ�����P��y���Ҳ���������ϣ������B���غ�ʱ����ֱ��д��ֱ��
����ֱ�ߵľ��붼��ȣ�����P��y���Ҳ���������ϣ������B���غ�ʱ����ֱ��д��ֱ��![]() �Ľ���ʽ����k��b���ú�m��ʽ�ӱ�ʾ��
�Ľ���ʽ����k��b���ú�m��ʽ�ӱ�ʾ��
���𰸡���1��![]() ��2����
��2����![]() ��
��![]() ����ֱ��l�Ľ���ʽΪ
����ֱ��l�Ľ���ʽΪ![]() ,
,![]() ��
��![]() .
.
��������
��1������һ�κ���ͼ���ϵ�����������������A��C�����꣬���ݵ�A��C�����꣬���ô���ϵ������������κ�������ʽ��
��2������PM��x��ɵó���PMC��90�����֡�MPC=90������PCM=90������������ǣ���i������MPC=90��ʱ��PC��x�ᣬ���ö��κ���ͼ���ϵ�����������������P�����ꣻ��ii������PCM=90��ʱ����PC��x�ύ�ڵ�D����֤��AOC�ס�COD���������������ε����ʿ������D�����꣬���ݵ�C��D�����꣬���ô���ϵ���������ֱ��PC�Ľ���ʽ������ֱ��PC�������ߵĽ���ʽ�ɷ����飬ͨ���ⷽ����������P�����꣮���ϣ����ʵý⣻
�����ö��κ���ͼ���ϵ������������һ�κ���ͼ���ϵ�����������ɵó���B��M�����꣬��ϵ�C������ɵó���B�������꣬���ݵ�M��B��B�������꣬���ô���ϵ�����ɷֱ����ֱ��BM��B��M��BB���Ľ���ʽ������ƽ���ߵ����ʿ����ֱ��l�Ľ���ʽ��
�⣺��1����![]() ʱ��
ʱ��![]() ��
��
![]() ��C������Ϊ
��C������Ϊ![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��ã�![]() ��
��
![]() ��A������Ϊ
��A������Ϊ![]() ��
��
��![]() ��
��![]() ����
����![]() ���ã�
���ã�
![]() ����ã�
����ã� ��
��
![]() �����ߵĽ���ʽΪ
�����ߵĽ���ʽΪ![]() ��
��
��2����![]() �ᣬ
�ᣬ
![]() ��
��
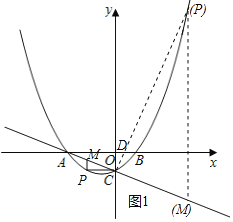
![]() ������������ǣ���ͼ1��ʾ��
������������ǣ���ͼ1��ʾ��
��i����![]() ʱ��
ʱ��![]() �ᣬ
�ᣬ
![]() ��P����������2��
��P����������2��
��![]() ʱ��
ʱ��![]() ��
��
��ã�![]() ��
��![]() ��
��
![]() ��P������Ϊ
��P������Ϊ![]() ��
��
��ii����![]() ʱ����PC��x�ύ�ڵ�D��
ʱ����PC��x�ύ�ڵ�D��
![]() ��
��![]() ��
��
![]() ��
��
��![]() ��
��
![]() ��
��
![]() ����
����![]() ��
��
![]() ��
��
![]() ��D������Ϊ
��D������Ϊ![]() ��
��
��ֱ��PC�Ľ���ʽΪ![]() ��
��
��![]() ��
��![]() ����
����![]() ���ã�
���ã�
![]() ����ã�
����ã�![]() ��
��
![]() ֱ��PC�Ľ���ʽΪ
ֱ��PC�Ľ���ʽΪ![]() ��
��
����ֱ��PC�������ߵĽ���ʽ�ɷ����飬�ã� ��
��
��ã�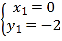 ��
��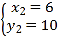 ��
��
��P������Ϊ![]() ��
��
������������![]() ��ֱ��������ʱ����P������Ϊ
��ֱ��������ʱ����P������Ϊ![]() ��
��![]() ��
��
�ڵ�y=0ʱ��![]() ,
,
��ã�x1=-4��x2=2��
���B��������2��0����
�ߵ�C������Ϊ��0��-2������B��B�����ڵ�C�Գƣ�
���B����������-2��-4����
�ߵ�P�ĺ�����Ϊm��m��0��m��2����
���M������Ϊ![]() ,
,
���ô���ϵ�����������ֱ��BM�Ľ���ʽΪ![]() ��ֱ��B��M�Ľ���ʽΪ
��ֱ��B��M�Ľ���ʽΪ![]() ��ֱ��BB���Ľ���ʽΪy=x-2��
��ֱ��BB���Ľ���ʽΪy=x-2��
������������ǣ���ͼ2��ʾ��
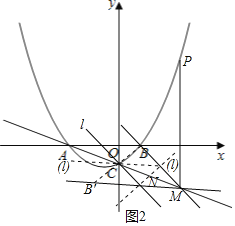
��ֱ��l��BM�ҹ���Cʱ��ֱ��l�Ľ���ʽΪ![]() ,
,
��ֱ��l��B��M�ҹ���Cʱ��ֱ��l�Ľ���ʽΪ![]() ,
,
��ֱ��l��BB���ҹ��߶�CM���е�![]() ʱ��ֱ��l�Ľ���ʽΪ
ʱ��ֱ��l�Ľ���ʽΪ![]() ,
,
����������ֱ��l�Ľ���ʽΪ![]() ,
,![]() ��
��![]() .
.

����Ŀ��С������ѧϰ�����ľ��飬�Ժ���![]() ��ͼ�������ʽ�����̽����������С����̽�����̣��벹�������������������⣺
��ͼ�������ʽ�����̽����������С����̽�����̣��벹�������������������⣺
��1������![]() ���Ա���x��ȡֵ��Χ�� ��
���Ա���x��ȡֵ��Χ�� ��
��2���±���y��x�ļ����Ӧֵ.
x | �� |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | �� |
y | �� |
|
|
| 2 |
| 4 |
| 2 |
|
| m | �� |
����m��ֵΪ________________��
��3����ͼ����ƽ��ֱ������ϵ�У���������ϱ��и��Զ�ӦֵΪ����ĵ�. ��������ĵ㣬��������![]() �Ĵ���ͼ��
�Ĵ���ͼ��
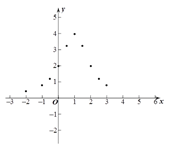
��4����Ϻ���ͼ����д������![]() ��һ�����ʣ�______________________.
��һ�����ʣ�______________________.
��5��������⣺�������![]() ��ֱ��y=a�Ľ�����2������ôa��ȡֵ��Χ��______________ .
��ֱ��y=a�Ľ�����2������ôa��ȡֵ��Χ��______________ .