题目内容
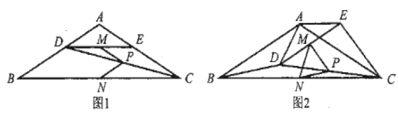
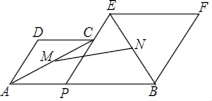
【题目】如图，已知AB＝8，P为线段AB上一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和PBFE，点P，C，E在一条直线上，∠DAP＝60°，M，N分别是对角线AC，BE的中点，当点P在线段AB上移动时，点M，N之间的距离最短为（ ）
A. 
B. 
C. 4D. 3
【答案】A
【解析】
连接PM、PN，推出∠MPN=60°+30°=90°，在Rt△PMN中利用勾股定理即可.
连接PM、PN．
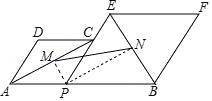
∵四边形APCD，四边形PBFE是菱形，∠DAP=60°，
∴∠APC=120°，∠EPB=60°，
∵M，N分别是对角线AC，BE的中点，
∴∠CPM=
∠APC=60°，∠EPN=∠EPB=30°，
∴∠MPN=60°+30°=90°，
设PA=2a，则PB=8﹣2a，PM=a，PN=
（4﹣a），
∴MN=
，
∴a=3时，MN有最小值，最小值为2，
故答案选：A．
练习册系列答案
相关题目
【题目】二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）的自变量x与函数值y的部分对应值如表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y＝ax2+bx+c | … | t | m | ﹣2 | ﹣2 | n | … |
且当x＝
时，与其对应的函数值y＞0，有下列结论：
①abc＜0；②m＝n；③﹣2和3是关于x的方程ax2+bx+c＝t的两个根；④
．
其中，正确结论的个数是（ ）.
A.1B.2C.3D.4
