题目内容

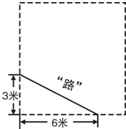
如图，在Rt△ABC中，∠C=90°，D为BC上一点，∠DAC=30°，BD=2，AB=2
3
，则AC的长为（　　）
A．
3
B．2
2
C．3D．
3
2
3

设CD=x，则AC=
CD
tan30°
=
x
3
3
=
3
x．
∵AC2+BC2=AB2，AC2+（CD+BD）2=AB2，
∴（
3
x）2+（x+2）2=（2
3
）2，
解得，x=1，∴AC=
3
．
故选A．
练习册系列答案
相关题目
如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是（　　）
A．48B．60C．76D．80
如图所示的是由3个边长为1的正方形组成的图形．
（1）则图中AB1=______，AB2=______，AB3=______
（2）从（1）中请你寻找规律，当图形是由10个正方形组成时，求AB10的值
（3）当图形有n个正方形组成时，求ABn的值．
如图，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，CD⊥AB于D，求CD的长．
在Rt△ABC中，∠C=90°，AC=8，BC=6，则AB边上的高为（　　）
A．4.8B．5.2C．4.5D．5.8
如图，在Rt△ABC中，∠C=90°，D为AC上一点，且DA=DB=5，又△DAB的面积为10，那么DC的长是（　　）
A．4B．3C．5D．4.5
如图所示，分别以直角三角形的三边为直径作半圆，其中两个半圆的面积S1=
25
8
π，S3=
9
8
π，则S2=______．
某园艺公司对一块直角三角形的花园进行改造，测得两直角边长分别为的=的米，b=8米．现要将其扩建成等腰三角形，且扩充部分是以b为直角边的直角三角形，则扩建后的等腰三角形花圃的周长为（　　）米．
A．32或20+4
5
B．32或36或
80
3
C．32或
80
3
或20+4
5
D．32或36或
80
3
或20+4
5
如图，学校有块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”，这些人只是大约少走了______步，却踩伤了花草．（一步约为0.75米，步数取整数）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网