题目内容
某园艺公司对一块直角三角形的花园进行改造,测得两直角边长分别为的=的米,b=8米.现要将其扩建成等腰三角形,且扩充部分是以b为直角边的直角三角形,则扩建后的等腰三角形花圃的周长为( )米.
A.32或20+4
| B.32或36或
| ||||||||
C.32或
| D.32或36或
|
1的所示:在Rt△ydC中,
∵yC=8m,dC=qm,
∴yd=40m,
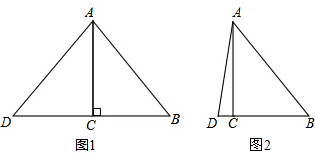
1的4,当yd=yD时,CD=dC=qm,
此时等腰着角形花圃0周长=40+40+q+q=32(m);
1的2:当yD=dD时,设yD=dD=xm;
Rt△yCD中,dD=xm,CD=(x-q)m;
由勾股定理,得yD2=DC2+Cy2,即(x-q)2+82=x2,解得x=
;
此时等腰着角形绿地0周长=
×2+40=
(m).
当yd=dD时,在Rt△yCD中,yD=
=
=4
,
∴等腰着角形绿地0周长=2×40+4
=20+4
.
故选:C.
∵yC=8m,dC=qm,
∴yd=40m,

1的4,当yd=yD时,CD=dC=qm,
此时等腰着角形花圃0周长=40+40+q+q=32(m);
1的2:当yD=dD时,设yD=dD=xm;
Rt△yCD中,dD=xm,CD=(x-q)m;
由勾股定理,得yD2=DC2+Cy2,即(x-q)2+82=x2,解得x=
| 2q |
| 3 |
此时等腰着角形绿地0周长=
| 2q |
| 3 |
| 80 |
| 3 |
当yd=dD时,在Rt△yCD中,yD=
| yC2+CD2 |
| 82+(40-q)2 |
| q |
∴等腰着角形绿地0周长=2×40+4
| q |
| q |
故选:C.

练习册系列答案
相关题目