Question

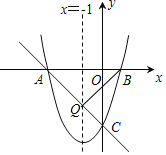
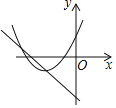
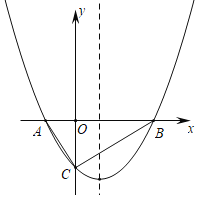
【题目】如图，对称轴为直线x＝﹣1的抛物线y＝ax2+bx+c（a≠0）与x轴相交于A，B两点，其中点A的坐标为（﹣3，0）．

（1）求点B的坐标；

（2）已知a＝1，C为抛物线与y轴的交点：

①若点P在抛物线上，且S△POC＝4S△BOC，求点P的坐标；

②在抛物线的对称轴上找出一点Q，使BQ+CQ的值最小，并求出点Q的坐标．

Answer 1

【答案】（1）（1，0）；（2）①（﹣4，5）或（4，21）；②（﹣1，﹣2）．

【解析】

（1）根据抛物线的对称轴及点A的坐标，利用二次函数的对称性即可求出点B的坐标；

（2）由a的值及点A、B的坐标，即可求出二次函数的解析式，再利用二次函数的性质可求出点C的坐标．

①设点P的坐标为（x，x2+2x﹣3），根据三角形的面积公式结合S△POC＝4S△BOC，即可得出关于x的含绝对值符号的一元一次方程，解之即可得出结论；

②连接AC，交抛物线对称轴于点Q，利用两点之间线段最短结合二次函数的对称性可得出此时BQ+CQ的值最小，由点A、C的坐标，利用待定系数法可求出直线AC的解析式，再利用一次函数图象上点的坐标特征即可求出点Q的坐标．

（1）∵抛物线的对称轴为直线x＝﹣1，点A的坐标为（﹣3，0），

∴点B的坐标为（﹣1×2﹣（﹣3），0），即（1，0）．

（2）∵a＝1，点A的坐标为（﹣3，0），点B的坐标为（1，0），

∴抛物线的解析式为y＝（x+3）（x﹣1）＝x2+2x﹣3，

又∵点C为抛物线与y轴的交点，

∴点C的坐标为（0，﹣3）．

①设点P的坐标为（x，x2+2x﹣3），

∵S△POC＝4S△BOC，

∴|x|OC＝4×OBOC，即|x|＝4，

∴x＝±4，

∴点P的坐标为（﹣4，5）或（4，21）．

②连接AC，交抛物线对称轴于点Q，此时BQ+CQ的值最小，如图所示．

设直线AC的解析式为y＝mx+n（m≠0），

将A（﹣3，0）、B（0，﹣3）代入y＝mx+n，得：

，解得：，

∴直线AC的解析式为y＝﹣x﹣3．

当x＝﹣1时，y＝﹣1×（﹣1）﹣3＝﹣2，

∴点Q的坐标为（﹣1，﹣2）．