Question

【题目】如图，在Rt△ABC中，AC＝6cm，BC＝8cm．点M从点A出发，以每秒1cm的速度沿AC方向运动：同时点N从点C出发，以每秒2cm的速度沿CB方向运动，当点N到达点B时，点M同时停止运动．

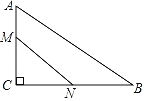
（1）运动几秒时，△CMN的面积为8cm2？

（2）△CMN的面积能否等于12cm2？若能，求出运动时间：若不能，请说明理由．

Answer 1

【答案】（1）2秒或4秒；（2）不能，理由见解析．

【解析】

（1）设运动t秒后△CMN的面积等于8cm2，分别表示出线段CM和线段CN的长，再利用三角形的面积公式列出方程求解即可；

（2）根据配方法可求△CMN的面积能否等于12cm2．

解：（1）设运动t秒后△CMN的面积等于8cm2，根据题意得：

CM＝6﹣t，CN＝2t，

则△CMN的面积是：

CMCN＝×（6﹣t）×2t＝8，

解得t1＝2，t2＝4，

故经过2秒或4秒后，△CMN的面积等于8cm2．

（2）△CMN的面积能否等于12cm2，

理由如下：

S△CMN=×（6﹣t）×2t＝﹣t2+6t＝﹣（t﹣3）2+9，

则当t＝3时，△CMN的面积最大为9，

∴△CMN的面积不能等于12cm2．