Question

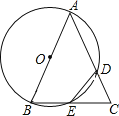
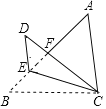
【题目】如图，在△ABC中，AB＞AC，∠B＝45°，AC＝5，BC＝4；E是AB边上一点，将△BEC沿EC所在直线翻折得到△DEC，DC交AB于F，当DE∥AC时，tan∠DCE的值为_____．

Answer 1

【答案】

【解析】

作CH⊥AB于H，EM⊥BC于M，在Rt△BHC中可求得 BH＝CH＝4，在Rt△AHC中运用勾股定理可求得AH=3，结合题意∠ACD＝∠D＝∠B＝45°，∠DCE＝∠BCE，由此可证明∠ACE=∠AEC，根据等角对等边AE=AC，所以BE=2，在Rt△BME中，可求得BM＝EM＝，从而根据线段的和差可求得MC，在Rt△EMC中根据正切的定义得解.

解：如图，作CH⊥AB于H，EM⊥BC于M，

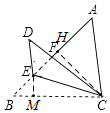
∵∠B＝45°，BC＝4，

∴BH＝CH＝4，

∵AC＝5，

∴AH＝3，

∴AB＝AH+BH＝3+4＝7，

∵将△BEC沿EC所在直线翻折得到△DEC，且DE∥AC，

∴∠ACD＝∠D＝∠B＝45°，∠DCE＝∠BCE，

∴∠ACE＝∠ACD+∠DCE＝∠B+∠BCE＝∠AEC，

∴AE＝AC＝5，

∴BE＝AB﹣AE＝7﹣5＝2，

∴BM＝EM＝，

∵BC＝4，

∴MC＝，

∴tan∠DCE＝．

故答案为：．