Question

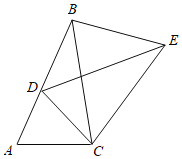
【题目】已知△ACB中，∠C=90°，以点A为中心，分别将线段AB, AC 逆时针旋转60°得到线段AD, AE,连接DE，延长DE交CB于点F.

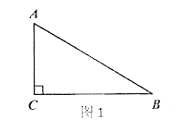
(1)如图1，若∠B=30°，∠CFE的度数为_________；

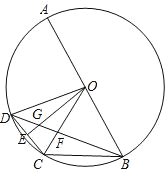
(2)如图2，当30°<∠B<60°时，

①依题意补全图2;

②猜想CF与AC的数量关系，并加以证明.

Answer 1

【答案】(1) 120°；(2)①作图见解析；②，证明见解析

【解析】

（1）先求出∠BAC=60°，进而判断出点E在边AB上，得出△ADE≌△ABC（SAS），进而得出∠AED=∠ACB=90°最后用三角形的外角的性质即可得出结论；

（2）①依题意补全图形即可；

②先判断出△ADE≌△ABC（SAS），进而得出∠AEF=90°，即可判断出Rt△AEF≌Rt△ACF，进而求出∠CAF=∠CAE=30°，即可得出结论．

解：（1）如图1，在Rt△ABC中，∠B=30°，

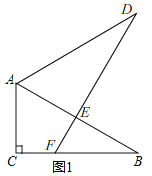
∴∠CAB=60°，

由旋转知，∠DAE=60°=∠CAB，

∴点E在边AB上，

∵AD=AB，AE=AC，

∴△ADE≌△ABC（SAS），

∴∠AED=∠ACB=90°，

∴∠CFE=∠B+∠BEF=30°+90°=120°，

故答案为120°；

（2）①依题意补全图形如图2所示，

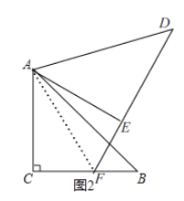
②如图2，连接AF，

∵∠BAD=∠CAE，

∴∠EAD=∠CAB，

∵AD=AB，AE=AC，

∴△ADE≌△ABC（SAS），

∴∠AED=∠C=90°，

∴∠AEF=90°，

∴Rt△AEF≌Rt△ACF，

∴∠EAF=∠CAF，

∴∠CAF=∠CAE=30°，

在Rt△ACF中，CF=AF，且AC2+CF2=AF2，

∴CF=AC．