题目内容
【题目】基本图形:在RT△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE.
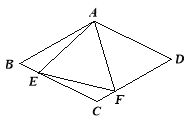
探索:(1)连接EC,如图①,试探索线段BC,CD,CE之间满足的等量关系,并证明结论;
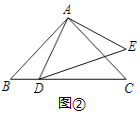
(2)连接DE,如图②,试探索线段DE,BD,CD之间满足的等量关系,并证明结论;
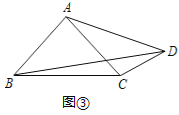
联想:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=7,CD=2,则AD的长为 .

【答案】(1)结论:![]() .证明见解析;(2)结论:
.证明见解析;(2)结论:![]() .证明见解析;(3)
.证明见解析;(3)![]()
【解析】
(1)说明△BAD≌OCAE(SAS)即可解答;
(2)先说明△BAD≌△CAE,可得BD=CE、∠ACE=∠B,进一步可得∠DCE=90°,最后利用勾股定理即可解答;
(3)作AE⊥AD.使AE=AD,连接CE,DE.由△BAD≌△CAE(SAS),推出BD=CE=7,由∠ADC=45°,∠EDA=45°,可得∠EDC=90°,最后利用勾股定理解答即可
解:(1)结论:![]() ,理由如下:
,理由如下:
如图①中,

∵![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() ;
;
(2)结论:![]() .理由如下:连接CE,
.理由如下:连接CE,

由(1)得,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]()
(3)作AE⊥4D,使4E=AD,连接CE,DE.
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD与△CAE中,
AB=AC,∠BAD=∠CAE,AD=AE
∴△BAD≌△CAE(SAS),
∴BD=CE=7,
∵∠ADC=45°,∠EDA=45°,
∴∠EDC=90°。
∴DE=![]() =√8.
=√8.
∵∠DAE=90°
∴![]() ,即
,即![]()
∴AD=![]() .
.
故答案为![]() .
.


练习册系列答案
相关题目