题目内容
【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.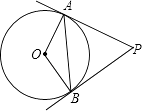
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
【答案】
(1)解:方法一:
∵在△ABO中,OA=OB,∠OAB=30°,
∴∠AOB=180°﹣2×30°=120°,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,
∴在四边形OAPB中,
∠APB=360°﹣120°﹣90°﹣90°=60°.
方法二:
∵PA、PB是⊙O的切线∴PA=PB,OA⊥PA;
∵∠OAB=30°,OA⊥PA,
∴∠BAP=90°﹣30°=60°,
∴△ABP是等边三角形,
∴∠APB=60°
(2)解:方法一:如图①,连接OP;
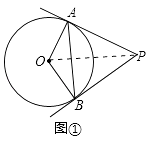
∵PA、PB是⊙O的切线,
∴PO平分∠APB,即∠APO= ![]() ∠APB=30°,
∠APB=30°,
又∵在Rt△OAP中,OA=3,∠APO=30°,
∴AP= ![]() =3
=3 ![]() .
.
方法二:如图②,作OD⊥AB交AB于点D;
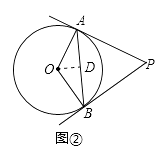
∵在△OAB中,OA=OB,
∴AD= ![]() AB;
AB;
∵在Rt△AOD中,OA=3,∠OAD=30°,
∴AD=OAcos30°= ![]() ,
,
∴AP=AB= ![]() .
.
【解析】(1) 方法一: 根据等边对等角及三角形的内角和得出∠AOB,再根据切线的性质及四边形的内角和得出答案;方法二:根据切线的性质及余角的定义得出△ABP是等边三角形,,从而得出结论;(2)方法一:如图①,连接OP; 利用切线的性质得出∠APO=30°,在Rt△OAP中,AP=![]() ,方法二:如图②,作OD⊥AB交AB于点D;根据等腰三角形的三线合一得出AD=
,方法二:如图②,作OD⊥AB交AB于点D;根据等腰三角形的三线合一得出AD= ![]() AB,在Rt△AOD中,AD=OAcos30°,从而得出结论。
AB,在Rt△AOD中,AD=OAcos30°,从而得出结论。

练习册系列答案
相关题目