Question

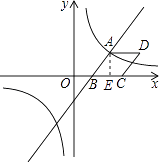
【题目】如图，已知一次函数y1= x﹣4与反比例函数y2= 的图象在第一象限相交于点A（6，n），与x轴相交于点B．
（1）填空：n的值为 ， k的值为；当y2≥﹣4时，x的取值范围是；
（2）以AB为边作菱形ABCD，使点C在点B右侧的x轴上，求点D的坐标．

Answer 1

【答案】
（1）4；24；x≤﹣6或x＞0
（2）解：由y1= . x﹣4=0，解得x=3，

∴B（3，0），

作AE⊥x轴于E，则E（6，0），AE=4，BE=3，

在Rt△ABE中，

AB= = =5，

边形ABCD是菱形，BC在x轴上，

∴AD=AB=5，AD∥x轴，

∴将点A向右移动5个单位长度得点D的坐标为（11，4）．

故答案为：4，24，x≤﹣6或x＞0．

【解析】解：（1）把点A（6，n）代入一次函数y1= x﹣4，可得n= ×6﹣4=4； 把点A（6，4）代入反比例函数y2= ，可得4= ，
解得k=24．
当y2=﹣4时，﹣4= ，解得x=﹣6．
故当y2≥﹣4时，自变量x的取值范围是x≤﹣6或x＞0．
【考点精析】掌握菱形的判定方法是解答本题的根本，需要知道任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形．