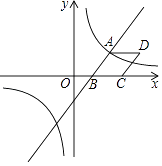Question

【题目】如图，在⊙O中，直径AB⊥CD，垂足为E，点M在OC上，AM的延长线交⊙O于点G，交过C的直线于F，∠1=∠2，连结CB与DG交于点N．
（1）求证：CF是⊙O的切线；
（2）求证：△ACM∽△DCN；
（3）若点M是CO的中点，⊙O的半径为4，cos∠BOC= ，求BN的长．

Answer 1

【答案】
（1）证明：∵△BCO中，BO=CO，

∴∠B=∠BCO，

在Rt△BCE中，∠2+∠B=90°，

又∵∠1=∠2，

∴∠1+∠BCO=90°，

即∠FCO=90°，

∴CF是⊙O的切线

（2）证明：∵AB是⊙O直径，

∴∠ACB=∠FCO=90°，

∴∠ACB﹣∠BCO=∠FCO﹣∠BCO，

即∠3=∠1，

∴∠3=∠2，

∵∠4=∠D，

∴△ACM∽△DCN

（3）解：∵⊙O的半径为4，即AO=CO=BO=4，

在Rt△COE中，cos∠BOC= ，

∴OE=COcos∠BOC=4× =1，

由此可得：BE=3，AE=5，由勾股定理可得：

CE= = = ，

AC= = =2 ，

BC= = =2 ，

∵AB是⊙O直径，AB⊥CD，

∴由垂径定理得：CD=2CE=2 ，

∵△ACM∽△DCN，

∴ = ，

∵点M是CO的中点，CM= AO= ×4=2，

∴CN= = = ，

∴BN=BC﹣CN=2 ﹣ = ．

【解析】（1）根据切线的判定定理得出∠1+∠BCO=90°，即可得出答案；（2）利用已知得出∠3=∠2，∠4=∠D，再利用相似三角形的判定方法得出即可；（3）根据已知得出OE的长，进而利用勾股定理得出EC，AC，BC的长，即可得出CD，利用（2）中相似三角形的性质得出NB的长即可．