题目内容
【题目】如图,矩形ABCD中,AB=6 cm,BC=8 cm,沿对角线AC将矩形分成两个直角三角形,其中△ABC不动,△A′C′D沿射线CA的方向以每秒2 cm的速度移动.
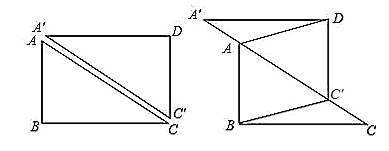
(1)在平移过程中,四边形ABC′D始终是 (请在下面的四个选项中选择一个你认为正确的序号填在横线上);
①平行四边形 ②矩形 ③菱形 ④正方形
(2)在移动过程中,当移动时间t(秒)为何值时,四边形ABC'D是菱形.
【答案】(1)①;(2)当t=![]() 秒时,四边形ABC′D是菱形.
秒时,四边形ABC′D是菱形.
【解析】则(1)直接利用平移的性质得出结论即可判断出四边形ABC'D是平行四边形;
(2)先根据勾股定理求出AC=10,再由菱形的性质得出BD⊥AC',OB=OD,AO=OC'.进而由直角三角形的 面积公式即可求出BO,再根据勾股定理求出AO,最后求出CC'即可求出时间.
(1)由平移得,AB=DC′,AB∥DC′,
∴四边形ABC′D是平行四边形,
故选①;
(2)如图,
,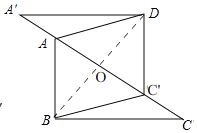
连接BD交AC于点O,
在Rt△ABC中,AB=6,BC=8,
∴AC=10,
∵四边形ABC′D是菱形,
∴BD⊥AC′,OB=OD,AO=OC′.
∵12ACBO=12ABBC,
∴BO=ABBCAC=6×810=245,
在Rt△ABO中,AB=6,BO=245,
∴AO=185,
∴C′O=AO=185,
∴AC′=AO+C′O=365,
∴CC′=ACAC′=10365=145,
∴t=145÷2=75,
当t=![]() 秒时,四边形ABC′D是菱形。
秒时,四边形ABC′D是菱形。

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目