ЬтФПФкШн
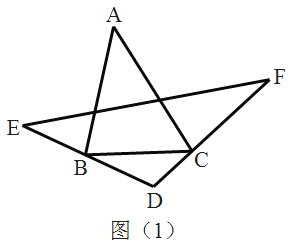
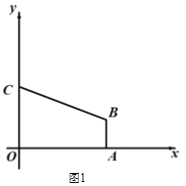
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжа,жБНЧЬнаЮOABCЕФЖЅЕуAЕФзјБъЮЊ(4ЃЌ0)ЃЌжБЯпy = -![]() x + 3ОЙ§ЖЅЕу BЃЌгыyжсНЛгкЖЅЕуCЃЌAB // OC.
x + 3ОЙ§ЖЅЕу BЃЌгыyжсНЛгкЖЅЕуCЃЌAB // OC.
(1)ЧѓЖЅЕуBЕФзјБъ.
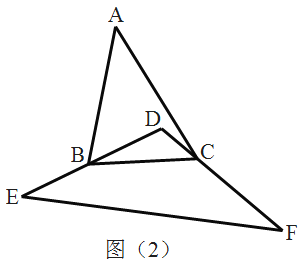
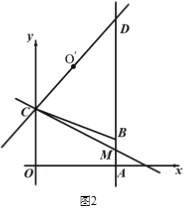
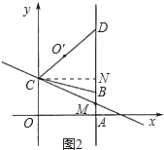
(2)Шч ЭМ2ЃЌжБЯп L ОЙ§Еу CЃЌгыжБЯп AB НЛгкЕу MЃЌЕу OЁфЮЊЕу O ЙигкжБЯпLЕФЖдГЦЕу,СЊ Нс COЁфЃЌВЂбгГЄНЛжБЯпABгкЕквЛЯѓЯоЕФЕу DЃЌЕБCD=5 ЪБЃЌЧѓжБЯп LЕФНтЮіЪНЃЛ
(3)дк(2)ЬѕМўЯТЃЌЕуPдкжБЯп LЩЯдЫЖЏЃЌЕуQдкжБЯпODЩЯдЫЖЏЃЌвд PЁЂQЁЂBЁЂC ЮЊЖЅЕуЕФЫФБпаЮФмЗёГЩЮЊЦНааЫФБпаЮЃПШєФм,ЧыжБНгаДГіЕуPзјБъЃЛШєВЛФмЃЌЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉB(4,2)ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉPЕузјБъЮЊЃЈ2,2ЃЉЛђЃЈ5,
ЃЛЃЈ3ЃЉPЕузјБъЮЊЃЈ2,2ЃЉЛђЃЈ5,![]() ЃЉЛђЃЈ-2,4ЃЉ.
ЃЉЛђЃЈ-2,4ЃЉ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЩшЕуBЕФзјБъЮЊ(4,y)ЃЌНЋx=4ДњШыжБЯпНтЮіЪНМДПЩЧѓГіBЕузнзјБъЃЌДгЖјЕУЕНBЕузјБъЃЛ
ЃЈ2ЃЉЙ§CЕузїCNЁЭABгкNЃЌгЩЦНааЯпКЭЖдГЦЕФаджЪПЩЭЦГіЁЯDCM=ЁЯDMCЃЌНјЖјЕУЕНCD=MD=5ЃЌРћгУЙДЙЩЖЈРэЧѓГіDNЃЌЕУЕНNM=2ЃЌвзЕУAM=1ЃЌДгЖјЕУЕНMЕузјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіжБЯпLЕФНтЮіЪНЃЛ
ЃЈ3ЃЉСЌНгODЃЌЯШЧѓГіODжБЯпНтЮіЪНЃЌИљОнЕуPдкжБЯп LЩЯдЫЖЏЃЌЕуQдкжБЯпODЩЯдЫЖЏЃЌПЩЩшPЕузјБъЮЊЃЈ![]() ЃЉЃЌQЕузјБъЮЊЃЈ
ЃЉЃЌQЕузјБъЮЊЃЈ![]() ЃЉЃЌдкЗжРрЬжТлЃЌРћгУЦНааЫФБпаЮЖдНЧЯпЛЅЯрЦНЗжЕФаджЪКЭжаЕузјБъЙЋЪНПЩНЈСЂЗНГЬЧѓНт.
ЃЉЃЌдкЗжРрЬжТлЃЌРћгУЦНааЫФБпаЮЖдНЧЯпЛЅЯрЦНЗжЕФаджЪКЭжаЕузјБъЙЋЪНПЩНЈСЂЗНГЬЧѓНт.
НтЃК(1)ЁпA(4,0)ЃЌABЁЮOCЃЌ
ЁрЩшЕуBЕФзјБъЮЊ(4,y)
Абx=4ДњШы![]() жаЃЌЕУy=2ЃЌ
жаЃЌЕУy=2ЃЌ
ЁрB(4,2)ЃЛ
(2)ШчЭМЃЌЙ§CЕузїCNЁЭABгкN,
ЁпABЁЮOCЃЌ
ЁрЁЯOCM=ЁЯDMCЃЌ
ЁпЕу OЁфЮЊЕу O ЙигкжБЯпLЕФЖдГЦЕу
ЁрЁЯDCM=ЁЯOCMЃЌ
ЁрЁЯDCM=ЁЯDMC
ЁрCD=MD=5ЃЌ
Ёп![]() ЃЌЕБx=0ЪБy=3ЃЌ
ЃЌЕБx=0ЪБy=3ЃЌ
ЁрOC=3ЃЌ
ЁпCN=OA=4ЃЌ
ЁрDN=![]() ЃЌ
ЃЌ
ЁрNM=53=2ЃЌ
ЁрAM=AN-NM=3-2=1
ЁрM(4,1)ЃЌ
ЩшжБЯпLНтЮіЪНy=kx+bАбC(0,3)ЃЌM(4,1)ДњШыЕУЃК
![]() ЃЌНтЕУ
ЃЌНтЕУ ЃЌ
ЃЌ
ЁржБЯпLЕФНтЮіЪНЮЊЃК![]() .
.
ЃЈ3ЃЉШчЭМЃЌСЌНгODЃЌ
ЁпAD=AM+MD=1+5=6ЃЌADЁЮOCЃЌAЕузјБъЮЊЃЈ4,0ЃЉ
ЁрDЕузјБъЮЊЃЈ4,6ЃЉ
ЩшODжБЯпНтЮіЪНЮЊ![]() ЃЌНЋЃЈ4,6ЃЉДњШыПЩЕУ
ЃЌНЋЃЈ4,6ЃЉДњШыПЩЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЁржБЯпODНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЁпЕуPдкжБЯп LЩЯдЫЖЏЃЌЕуQдкжБЯпODЩЯдЫЖЏ
ЁрЩшPЕузјБъЮЊЃЈ![]() ЃЉЃЌQЕузјБъЮЊЃЈ
ЃЉЃЌQЕузјБъЮЊЃЈ![]() ЃЉЃЌ
ЃЉЃЌ
ЗжЧщПіЬжТлЃК
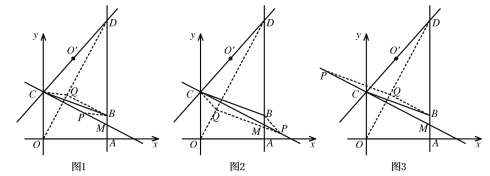
ШчЭМ1ЫљЪОЃЌЕБBCЁЂPQЮЊЖдНЧЯпЪБЃЌгЩЦНааЫФБпаЮЖдНЧЯпЛЅЯрЦНЗжЕФаджЪКЭжаЕузјБъЙЋЪНПЩЕУЃК
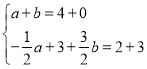 ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЁрPЕузјБъЮЊЃЈ2,2ЃЉЃЛ
ШчЭМ2ЫљЪОЃЌЕБBQЁЂPCЮЊЖдНЧЯпЪБЃЌЭЌРэПЩЕУЃК
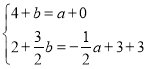 ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЁрPЕузјБъЮЊЃЈ5,![]() ЃЉЃЛ
ЃЉЃЛ
ШчЭМ3ЫљЪОЃЌЕБBPЁЂCQЮЊЖдНЧЯпЪБЃЌЭЌРэПЩЕУЃК
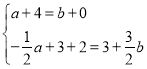 ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЁрPЕузјБъЮЊЃЈ-2,4ЃЉЃЛ
злЩЯЫљЪіЃЌPЕузјБъЮЊЃКЃЈ2,2ЃЉЛђЃЈ5,![]() ЃЉЛђЃЈ-2,4ЃЉ.
ЃЉЛђЃЈ-2,4ЃЉ.

 злКЯздВтЯЕСаД№АИ
злКЯздВтЯЕСаД№АИ