Question

【题目】阅读理解：如图1，在的边上取一点，连接，可以把分成两个三角形，如果这两个三角形都是等腰三角形，我们就称点是的边上的和谐点．

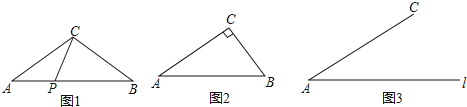
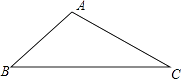
（1）如图2，在中，，试找出边上的和谐点；

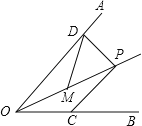
（2）如图3，已知，的顶点在射线上，点是边上的和谐点，请在图3中画出所有符合条件的点，并写出相应的的度数．

Answer 1

【答案】（1）AB边上的和谐点为AB的中点；（2）∠B的度数为35°、50°、80°、20°．

【解析】

（1）由直角三角形斜边上的中线等于斜边的一半，找出和谐点为斜边的中点；

（2）由∠A为等腰三角形的顶角和底角分类讨论得出符合条件的点B，继而可写出∠B的度数.

（1）AB边上的和谐点为AB的中点，理由如下：

∵P是AB的中点，

∴PC=AB=PA=PB，

∴△ACP和△BCP是等腰三角形；

（2）①当∠A=∠ACP=40°时，则CPB=40°+40°=80°，如图：

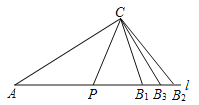
若CP=CB1，则∠CPB1=∠CB1P=80°，

若B2P=B2C，则∠B2PC=B2CP=80°，所以∠B2=180°﹣80°﹣80°=20°，

若PC=B3P，则∠PCB3=PB3C==50°；

②当∠A=∠APC=40°时，如图：

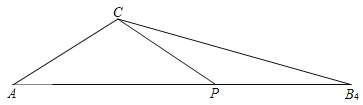
∵∠CPB4=180°﹣∠APC=180°﹣40°=140°，

∴∠B4==20°；

③当∠ACP=∠APC=70°时，如图：

∵∠CPB5=180°﹣∠APC=180°﹣70°=110°，

∴∠B==35°，

综上所述，符合条件的∠B的度数为35°、50°、80°、20°．