Question

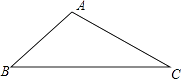
【题目】已知△ABC中，AB＝AC，∠BAC＝90°．

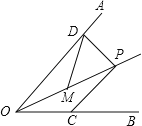
（1）如图，若CD平分∠ACB，BE⊥CD，垂足E在CD的延长线上，试探究线段BE和CD的数量关系，并证明你的结论

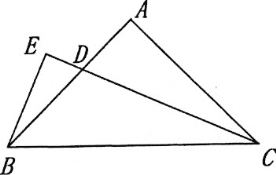
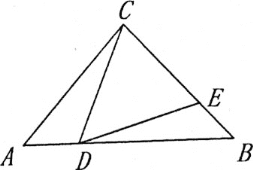
（2）如图，若点D在线段BC延长上，BE⊥DE，垂足为E，DE与AB相交于点F．试探究线段BE和FD的数量关系，并证明你的结论．

Answer 1

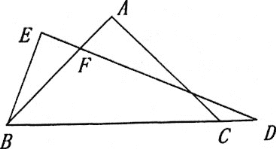
【答案】（1）CD=2BE，证明见解析；（2）DF=2BE，证明见解析.

【解析】

（1）如图，证明△ABF≌△ACD，得CD=BF，则2BE=CD；
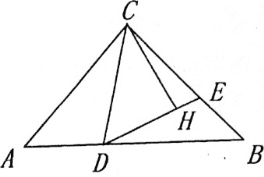
（2）如图，同（1）作辅助线，证明△BHG≌△DHF得DF=BG=2BE．

(1) 延长BE、CA交于点E

∵CE⊥BF, CD平分∠ACB

∴△BCE为等腰三角形, ∴BF=2BE

易证∠ACD＝∠ABF

在△ABF和△ACD中

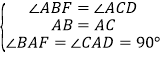
∴△ABF≌△ACD…………………5分

∴CD＝BF=2BE.

(2)过D作DG∥AC交BE的延长线于G,BA的延长线于H

∴∠GDB＝∠ACB=∠ABC

BH=DH

同（1）法证在△BHG≌△DHF得DF=BG=2BE.

.