题目内容
 已知:如图,直线a、b被c所截;∠1、∠2是同位角,且∠1≠∠2,
已知:如图,直线a、b被c所截;∠1、∠2是同位角,且∠1≠∠2,
求证:a不平行b.
证明:假设________,
则________,(两直线平行,同位角相等)
这与________相矛盾,所以________不成立,
故a不平行b.
a∥b ∠1=∠2 已知∠1≠∠2 假设
分析:根据已知条件与平行线的性质填空.
解答:证明:假设a∥b,∴∠1=∠2,(两直线平行,同位角相等.),与已知∠1≠∠2相矛盾,
∴假设不成立,
∴a不平行b.每空
点评:本题利用反证法证明两直线不平行,实际上仍然是运用平行线的性质.
分析:根据已知条件与平行线的性质填空.
解答:证明:假设a∥b,∴∠1=∠2,(两直线平行,同位角相等.),与已知∠1≠∠2相矛盾,
∴假设不成立,
∴a不平行b.每空
点评:本题利用反证法证明两直线不平行,实际上仍然是运用平行线的性质.

练习册系列答案
相关题目
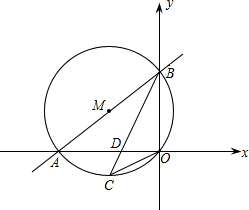 原点O及A、B两点.
原点O及A、B两点.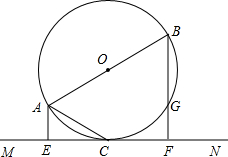 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦,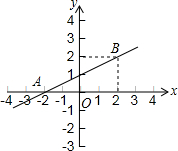 已知:如图,直线y=kx+b经过点A、B.
已知:如图,直线y=kx+b经过点A、B.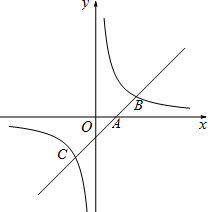 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线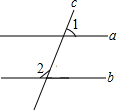 已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x-5)°,那么∠1=
已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x-5)°,那么∠1=