题目内容
 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=| m |
| x |
(1)求直线y=kx+b和双曲线y=
| m |
| x |
(2)根据图象写出关于x的不等式kx+b<
| m |
| x |
(3)点D在直线y=kx+b上,设点D的纵坐标为t(t>0).过点D作平行于x轴的直线交双曲线y=
| m |
| x |
| 7 |
| 2 |
分析:(1)先把点B的坐标代入反比例函数y=
求出m的值,故可得出反比例函数的解析式,再把C点坐标代入反比例函数的解析式即可求出n的值,用待定系数法求出直线y=kx+b的解析式即可;
(2)直接根据两函数图象的交点即可求出x的取值范围;
(3)由于DE的位置关系不能确定,故应分点D在点E的右方与点D在点E的左方两种情况进行讨论.
| m |
| x |
(2)直接根据两函数图象的交点即可求出x的取值范围;
(3)由于DE的位置关系不能确定,故应分点D在点E的右方与点D在点E的左方两种情况进行讨论.
解答:解:(1)∵双曲线y=
经过点B(4,2),
∴2=
,解得m=8.
∴双曲线的解析式为y=
.
∵点C(n,-4)在双曲线y=
上,
∴-4=
,n=-2.
∵直线y=kx+b经过点B(4,2),C(-2,-4),
则
解得
∴直线的解析式为y=x-2.
(2)由函数图象可知x<-2或0<x<4直线y=x-2的图象在反比例函数图象的下方,故x<-2或0<x<4;
(3)∵点D在直线y=x-2上,且点D的纵坐标为t(t>0),
∴D(t+2,t),
∵DE∥x轴,点E在双曲线y=
上,
∴E(
,t),
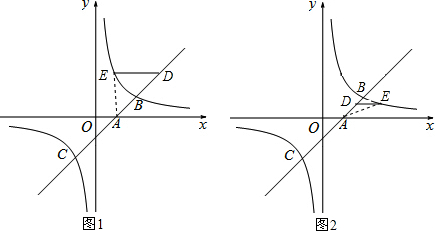
当点D在点E的右方,即如图1所示时,
S△ADE=
(t+2-
)•t=
,解得t=3或t=-5(舍去);
当点D在点E的左方,即如图2所示时,
S△ADE=
(
-t-2)•t=
,解得t=
-1或t=-1-
(舍去);
故t=3或
-1.
| m |
| x |
∴2=
| m |
| 4 |
∴双曲线的解析式为y=
| 8 |
| x |
∵点C(n,-4)在双曲线y=
| 8 |
| x |
∴-4=
| 8 |
| n |
∵直线y=kx+b经过点B(4,2),C(-2,-4),
则
|
|
∴直线的解析式为y=x-2.
(2)由函数图象可知x<-2或0<x<4直线y=x-2的图象在反比例函数图象的下方,故x<-2或0<x<4;
(3)∵点D在直线y=x-2上,且点D的纵坐标为t(t>0),
∴D(t+2,t),
∵DE∥x轴,点E在双曲线y=
| 8 |
| x |
∴E(
| 8 |
| t |
当点D在点E的右方,即如图1所示时,
S△ADE=
| 1 |
| 2 |
| 8 |
| t |
| 7 |
| 2 |
当点D在点E的左方,即如图2所示时,
S△ADE=
| 1 |
| 2 |
| 8 |
| t |
| 7 |
| 2 |
| 2 |
| 2 |
故t=3或
| 2 |

点评:本题考查的是反比例函数综合题,熟知用待定系数法求一次函数及反比例函数的解析式是解答此题的关键.

练习册系列答案
相关题目
 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b经过点A、B.
已知:如图,直线y=kx+b经过点A、B. 已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x-5)°,那么∠1=
已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x-5)°,那么∠1=