题目内容
(2002•岳阳)已知:如图,直线MN和⊙O切于点C,AB是⊙O的直径,AE⊥MN,BF⊥MN且与⊙O 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦,
(1)求证:AB=AE+BF;
(2)令AE=m,EF=n,BF=p,证明:n2=4mp;
(3)设⊙O的半径为5,AC=6,求以AE、BF的长为根的一元二次方程;
(4)将直线MN向上平行移动至与⊙O相交时,m、n、p之间有什么关系?向下平行移动至与⊙O相离时,m、n、p之间又有什么关系?
 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦,(1)求证:AB=AE+BF;
(2)令AE=m,EF=n,BF=p,证明:n2=4mp;
(3)设⊙O的半径为5,AC=6,求以AE、BF的长为根的一元二次方程;
(4)将直线MN向上平行移动至与⊙O相交时,m、n、p之间有什么关系?向下平行移动至与⊙O相离时,m、n、p之间又有什么关系?
分析:(1)连接OC,先利用AE、BF都垂直于MN,而AB≠EF,可证四边形ABFE是梯形,而O是AB中点,且AE∥OC∥BF,利用平行线分线段成比例定理的推论,易得CE:CF=AO:BO,那么C也是EF中点,从而OC使梯形中位线,利用梯形中位线定理可证AE+BF=2OC,而AB=2OC,即可证;
(2)连接AC、BC,AB是直径,易得∠ACB是90°,从而∠ACE+∠FCB=90°,而BF⊥MN,易得∠FCB+∠FBC=90°,利用同角的余角相等,可证∠ECA=∠FBC,再加上一对直角相等,容易证出△EAC∽△FCB,可得比例线段,再结合CE=CF=
EF,代入比例线段,化简即可得证.
(3)由(2)可求得AE+BF=10,又由勾股定理与相似三角形的性质,求得AE与BF的长,继而求得AE•BF,即可得以AE、BF的长为根的一元二次方程;
(4)根据题意画出图形,由平移可得四边形EFF′E′是矩形,即可得EF=E′F′,又由EF2=4AE•BF,即可求得答案.
(2)连接AC、BC,AB是直径,易得∠ACB是90°,从而∠ACE+∠FCB=90°,而BF⊥MN,易得∠FCB+∠FBC=90°,利用同角的余角相等,可证∠ECA=∠FBC,再加上一对直角相等,容易证出△EAC∽△FCB,可得比例线段,再结合CE=CF=
| 1 |
| 2 |
(3)由(2)可求得AE+BF=10,又由勾股定理与相似三角形的性质,求得AE与BF的长,继而求得AE•BF,即可得以AE、BF的长为根的一元二次方程;
(4)根据题意画出图形,由平移可得四边形EFF′E′是矩形,即可得EF=E′F′,又由EF2=4AE•BF,即可求得答案.
解答:(1)证明:连接OC,
∵AE⊥MN,BF⊥MN,
∴AE∥BF,而AB≠EF,
∴四边形ABFE为梯形,
∵直线MN和⊙O切于点C,
∴OC⊥MN,
∴OC∥AE∥BF,
∴OA=OB,
∴OC为梯形ABFE的中位线,
∴AE+BF=2OC,
即:AB=AE+BF;
(2)证明:连接BC,
∵AB是直径,
∴∠ACB=90°,
∴∠ECA+∠FCB=90°,
∵∠CBF+∠FCB=90°,
∴∠CBF=∠ECA,
∵∠AEC=∠BFC=90°,
∴△AEC∽△CFB,
∴EC:BF=AE:CF,
∴CF•EC=AE•BF,
∵CF=EC=
EF,
∴EF2=4AE•BF,
∵AE=m,EF=n,BF=p,
∴n2=4mp;
(3)解:∵AB=AE+BF,⊙O的半径为5,AC=6,
∴AE+BF=10,BC=
=8,
∵△AEC∽△CFB,
∴AC:BC=EC:BF=6:8=3:4,
∵EC=FC,
∴CF:BF=3:4,
设CF=3x,BF=4x,
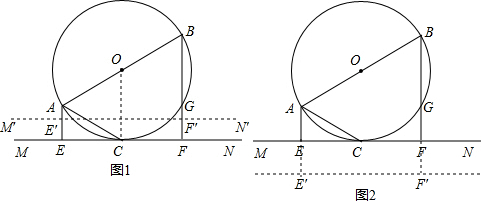 则(3x)2+(4x)2=64,
则(3x)2+(4x)2=64,
解得:x=
,
即BF=
,
∴AE=10-
=
,
∴AE•BF=
,
∴以AE、BF的长为根的一元二次方程为:x2-
x+10=0;
(4)解:由平移的性质,可得:四边形EFF′E′是矩形,
∴E′F′=EF,
∵EF2=4AE•BF,
∴E′F′2=4AE•BF,
∴n2=4mp;
∴将直线MN向上平行移动至与⊙O相交时,m、n、p之间的关系为:n2=4mp;向下平行移动至与⊙O相离时,m、n、p之间的关系为:n2=4mp.
∵AE⊥MN,BF⊥MN,
∴AE∥BF,而AB≠EF,
∴四边形ABFE为梯形,
∵直线MN和⊙O切于点C,
∴OC⊥MN,

∴OC∥AE∥BF,
∴OA=OB,
∴OC为梯形ABFE的中位线,
∴AE+BF=2OC,
即:AB=AE+BF;
(2)证明:连接BC,
∵AB是直径,
∴∠ACB=90°,
∴∠ECA+∠FCB=90°,
∵∠CBF+∠FCB=90°,
∴∠CBF=∠ECA,
∵∠AEC=∠BFC=90°,
∴△AEC∽△CFB,
∴EC:BF=AE:CF,
∴CF•EC=AE•BF,
∵CF=EC=
| 1 |
| 2 |
∴EF2=4AE•BF,
∵AE=m,EF=n,BF=p,
∴n2=4mp;
(3)解:∵AB=AE+BF,⊙O的半径为5,AC=6,
∴AE+BF=10,BC=
| AB2-AC2 |
∵△AEC∽△CFB,
∴AC:BC=EC:BF=6:8=3:4,
∵EC=FC,
∴CF:BF=3:4,
设CF=3x,BF=4x,
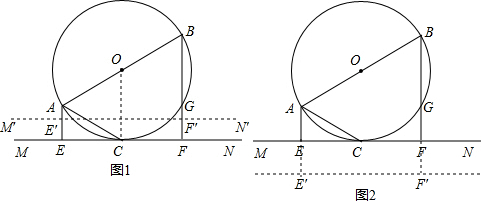 则(3x)2+(4x)2=64,
则(3x)2+(4x)2=64,解得:x=
| 8 |
| 5 |
即BF=
| 32 |
| 5 |
∴AE=10-
| 32 |
| 5 |
| 18 |
| 5 |
∴AE•BF=
| 576 |
| 25 |
∴以AE、BF的长为根的一元二次方程为:x2-
| 576 |
| 25 |
(4)解:由平移的性质,可得:四边形EFF′E′是矩形,
∴E′F′=EF,
∵EF2=4AE•BF,
∴E′F′2=4AE•BF,
∴n2=4mp;
∴将直线MN向上平行移动至与⊙O相交时,m、n、p之间的关系为:n2=4mp;向下平行移动至与⊙O相离时,m、n、p之间的关系为:n2=4mp.
点评:此题考查了切线的性质、相似三角形的判定与性质、一元二次方程根与系数的关系以及平移的性质.此题综合性较强,难度较大,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
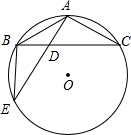 (2002•岳阳)已知:如图,△ABC内接于⊙O,AB=AC=
(2002•岳阳)已知:如图,△ABC内接于⊙O,AB=AC=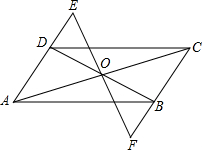 (2002•岳阳)如图,已知?ABCD的对角线AC、BD相交于点O,过点O任作一直线分别交AD、CB的延长线于E、F,求证:OE=OF.
(2002•岳阳)如图,已知?ABCD的对角线AC、BD相交于点O,过点O任作一直线分别交AD、CB的延长线于E、F,求证:OE=OF. AB=2,又关于x的方程x2-(b+2ac)x+m=0(m<0)的两个实数根互为相反数.
AB=2,又关于x的方程x2-(b+2ac)x+m=0(m<0)的两个实数根互为相反数.