题目内容
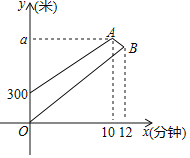
【题目】如图,在平面直角坐标系中,矩形![]() 的边
的边![]() 在
在![]() 轴上,
轴上,![]() 、
、![]() 的长分别是一元二次方程
的长分别是一元二次方程![]() 的两个根
的两个根![]() ,
,![]() ,边
,边![]() 交
交![]() 轴于点
轴于点![]() ,动点
,动点![]() 以每秒
以每秒![]() 个单位长度的速度,从点
个单位长度的速度,从点![]() 出发沿折线段
出发沿折线段![]() 向点
向点![]() 运动,运动的时间为
运动,运动的时间为![]() 秒,设
秒,设![]() 与矩形
与矩形![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求![]() 关于
关于![]() 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(3)在点![]() 的运动过程中,是否存在
的运动过程中,是否存在![]() ,使
,使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)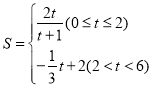 (3)
(3)![]() 或
或![]() 或
或![]()
【解析】
(1)解方程求出x的值,由BC>AB,OA=2OB可得答案;
(2)设BP交y轴于点F,当0≤t≤2时,PE=t,由△OBF∽△EPF知![]()
,即![]() ,据此得
,据此得![]() ,根据面积公式可得此时解析式;当2<t<6时,AP=6-t,由△OBF∽△ABP知
,根据面积公式可得此时解析式;当2<t<6时,AP=6-t,由△OBF∽△ABP知![]() ,即
,即![]() ,据此得
,据此得![]() ,根据三角形面积公式可得答案;
,根据三角形面积公式可得答案;
(3)设P(-2,m),由B(1,0),E(0,4)知![]() ,
, ![]() ,
,![]() ,再分三种情况列出方程求解可得.
,再分三种情况列出方程求解可得.
(1)![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
(2)设![]() 交
交![]() 轴于点
轴于点![]() ,
,
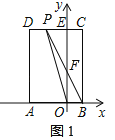
如图1,当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ;
;
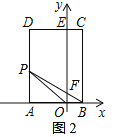
如图2,当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
![]()
![]() ;
;
综上所述,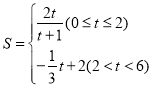 ;
;
(3)由题意知,当点![]() 在
在![]() 上时,显然不能构成等腰三角形;
上时,显然不能构成等腰三角形;
当点![]() 在
在![]() 上运动时,设
上运动时,设![]() ,
,
![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,解得
,解得![]() ,
,
则![]() ;
;
②当![]() 时,
时,![]() ,解得
,解得![]() ,
,
则 ![]() ;
;
③当![]() 时,
时,![]() ,解得
,解得![]() ,
,
则![]() ;
;
综上,![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目