题目内容
【题目】定义:到三角形的两边距离相等的点,叫做此三角形的准内心.

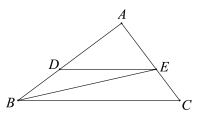
(1)求证:等腰三角形底边的中点是它的准内心;
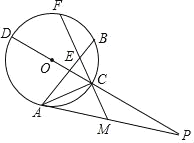
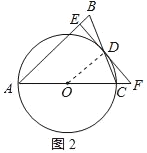
(2)如图,在△ABC中,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线EF,分别交AB与AC的延长线于点E,F.若点D是△ABC的准内心,AE=6,tan∠CFD=![]() ,求EB的长.
,求EB的长.
【答案】(1)见解析;(2)EB=![]()
【解析】
(1)要证等腰三角形底边的中点是它的准内心即证明底边中点到两腰的距离相等,添加辅助线,作DM⊥AB于M,DN⊥AC于N,依据等腰三角形的性质,结合已知条件可判断出△BDM≌△CDN,即可知DM=DN,结论得证;(2)由图可知EB=AB﹣AE,题中已知AE=6,故只用求出AB即可,因为tan∠CFD=![]() ,很明显需要直角三角形,因此可连接OD,EF是⊙O的切线,所以OD⊥EF,出现直角,而已知的边是AE的长可以证明AE⊥EF,根据正切值可求出EF长,由勾股定理求出AF长,显然,OD∥AB,可得△ODF∽△AEF,相似三角形对应线段成比例即可求出OD长,AB长可相应得出.
,很明显需要直角三角形,因此可连接OD,EF是⊙O的切线,所以OD⊥EF,出现直角,而已知的边是AE的长可以证明AE⊥EF,根据正切值可求出EF长,由勾股定理求出AF长,显然,OD∥AB,可得△ODF∽△AEF,相似三角形对应线段成比例即可求出OD长,AB长可相应得出.
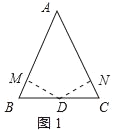
(1)已知:△ABC中,AB=AC,D是BC的中点,
求证:D是△ABC的准内心;
证明:DM⊥AB于M,DN⊥AC于N,如图1所示:
则∠DMB=∠DNC=90°,
∵AB=AC,
∴∠B=∠C,
∵D是BC的中点,
∴BD=CD,
在△BDM和△CDN中,
 ,
,
∴△BDM≌△CDN(AAS),
∴DM=DN,
∴D是△ABC的准内心;
(2)连接OD,如图2所示:
∵OA=OC=OD,
∴OD=![]() AC,
AC,
∵点D是△ABC的准内心,
∴点D到AB、AC的距离相等,
∴∠BAD=∠CAD,
∵AC是⊙O的直径,
∴∠ADB=∠ADC=90°,
∴∠B=∠C,
∴AB=AC,
∴BD=CD,
∵OA=OC,
∴OD是△ABC的中位线,
∴OD∥AB,
∵EF是⊙O的切线,
∴OD⊥EF,
∴AB⊥EF,
∵tan∠CFD=![]() =
=![]() ,
,
∴EF=![]() =8,
=8,
∴AF=![]() =10,
=10,
∵OD∥AB,
∴△ODF∽△AEF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:OD=![]() ,
,
∴AB=AC=2OD=![]() ,
,
∴EB=AB﹣AE=![]() ﹣6=
﹣6=![]() .
.

【题目】某教学网站策划了![]() 、
、![]() 两种上网学习的月收费方式:
两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 月包时上网时间/ | 月超时费/(元/ |
| 7 | 25 | 0.6 |
| 10 | 50 | 3 |
设每月上网学习的时间为![]() .
.
(Ⅰ)根据题意,填写下表:
月使用费/元 | 月上网时间/ | 月超时费/元 | 月总费用/元 | |
方式 | 7 | 45 | ||
方式 | 10 | 45 |
(Ⅱ)设![]() ,
,![]() 两种方式的收费金额分别为
两种方式的收费金额分别为![]() 元和
元和![]() 元,分别写出
元,分别写出![]() ,
,![]() 与
与![]() 的函数解析式;
的函数解析式;
(Ⅲ)当![]() 时,你认为哪种收费方式省钱?请说明理由.
时,你认为哪种收费方式省钱?请说明理由.