题目内容
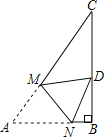
【题目】如图，
为
的直径，
平分
，交弦
于点
，连接半径
交于点
，过点
的一条直线交的延长线于点
，
．
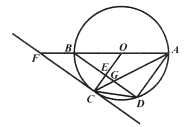
（1）求证：直线
是的切线；
（2）若
．
①求
的长；
②求
的周长．（结果可保留根号）
【答案】（1）见解析；（2）①
，②
.
【解析】
(1)先证明
，继而推导得出
即可；
(2)①设
，在
中，利用勾股定理求出R的值，继而求出OE的长，进而根据三角形中位线定理即可求得AD长；
②连接
，证明△OBE∽△OFC，根据相似三角形对应边成比例可求得
，
，进而得
，在
中，利用勾股定理求得BC长，继而求出AC长即可求得答案.
(1)
平分
，
，
是弧
的中点，
，
，
，
，
，
，
，
是半径，
是圆
切线；
(2)①设，
，
，
，
，
在中，
，
解得
，
，
由(1)得，
，
，
；
②连接.
，
∴△OBE∽△OFC，
，
，
，，
，，
，
在中，，
，
，
是直径，
为直角三角形，
，
周长
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某教学网站策划了
、
两种上网学习的月收费方式：
收费方式 | 月使用费/元 | 月包时上网时间/ | 月超时费/（元/ |
| 7 | 25 | 0.6 |
| 10 | 50 | 3 |
设每月上网学习的时间为
.
（Ⅰ）根据题意，填写下表：
月使用费/元 | 月上网时间/ | 月超时费/元 | 月总费用/元 | |
方式 | 7 | 45 | ||
方式 | 10 | 45 |
（Ⅱ）设，两种方式的收费金额分别为
元和
元，分别写出，与
的函数解析式；
（Ⅲ）当
时，你认为哪种收费方式省钱？请说明理由.
