题目内容
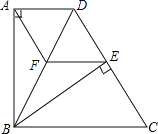
【题目】如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F,AD=12,DC=18.
(1)证明:△ADF≌△AB′E;
(2)求线段AF的长度.
(3)求△AEF的面积.

【答案】(1)见解析;(2)13;(3)78.
【解析】
(1)根据折叠的性质以及矩形的性质,运用ASA即可判定△ADF≌△AB′E;
(2)先设FA=FC=x,则DF=DC﹣FC=18﹣x,根据Rt△ADF中,AD2+DF2=AF2,即可得出方程122+(18﹣x)2=x2,然后解关于x的值即可;
(3)由S△AEF=![]() AEAD求解即可.
AEAD求解即可.
解:(1)∵四边形ABCD是矩形,
∴∠D=∠C=∠B′=90°,AD=CB=AB′,
∵∠DAF+∠EAF=90°,∠B′AE+∠EAF=90°,
∴∠DAF=∠B′AE,
在△ADF和△AB′E中, ,
,
∴△ADF≌△AB′E(ASA).
(2)由折叠性质得FA=FC,
设FA=FC=x,则DF=DC﹣FC=18﹣x,
在Rt△ADF中,AD2+DF2=AF2,
∴122+(18﹣x)2=x2.
解得x=13.
∵△ADF≌△AB′E(已证),
∴AE=AF=13,
(3)S△AEF=![]() ×12×13=78.
×12×13=78.

练习册系列答案
相关题目
【题目】用火柴棒按下列方式搭建三角形:
![]()
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | 3 | 5 | 7 | 9 | … |
(1)当三角形的个数为n时,火柴棒的根数是多少?
(2)求当n=100时,有多少根火柴棒?
(3)当火柴棒的根数为2017时,三角形的个数是多少?