题目内容
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

【答案】(1)相切,证明见解析;(2)6![]() .
.
【解析】
(1)欲证明CD是切线,只要证明OD⊥CD,利用全等三角形的性质即可证明;
(2)设⊙O的半径为r.在Rt△OBE中,根据OE2=EB2+OB2,可得(8﹣r)2=r2+42,推出r=3,由tan∠E=![]() ,推出
,推出![]() ,可得CD=BC=6,再利用勾股定理即可解决问题.
,可得CD=BC=6,再利用勾股定理即可解决问题.
(1)相切,理由如下,
如图,连接OC,
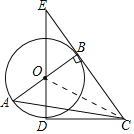
∵CB=CD,CO=CO,OB=OD,
∴△OCB≌△OCD,
∴∠ODC=∠OBC=90°,
∴OD⊥DC,
∴DC是⊙O的切线;
(2)设⊙O的半径为r,
在Rt△OBE中,∵OE2=EB2+OB2,
∴(8﹣r)2=r2+42,
∴r=3,AB=2r=6,
∵tan∠E=![]() ,
,
∴![]() ,
,
∴CD=BC=6,
在Rt△ABC中,AC=![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】我市合江县先滩乡出产的香米口感香糯,包装质量为每袋![]() 千克,县粮油公司应成都某粮油公司要求抽取
千克,县粮油公司应成都某粮油公司要求抽取![]() 袋样品进行检测,称重结果如下表(单位:千克):
袋样品进行检测,称重结果如下表(单位:千克):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)为了简化运算,可选取一个恰当的基准数_________,用正、负数填写下表:
原质量 |
|
|
|
|
|
|
|
|
|
|
与基准数的差距 |
(2)根据这个表,计算这![]() 袋先滩香米的总质量.
袋先滩香米的总质量.