题目内容
【题目】如图，直线
分别与x，y轴交于
、B两点，过点B的直线交x轴负半轴于C，且
．
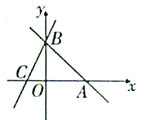
（1）求点B的坐标；
（2）求直线BC的解析式．
【答案】(1) B点坐标为：(0,6)；(2) 直线BC的解析式为：y=3x+6.
【解析】
（1）首先将B点坐标代入y=-x-b求出b的值，进而求出B点坐标；
（2）利用OB：OC=3：1，得出C点坐标，再利用待定系数法求一次函数解析式．
(1)∵直线AB: y=xb分别与x，y轴交于A(6,0)、B两点，
∴0=6b，
解得：b=6，
则y=x+6，
当x=0，则y=6，
故B点坐标为：(0,6)；
(2)∵OB:OC=3:1，
∴CO=2，
则C点坐标为：(2,0)，
将B，C点代入直线BC的解析式y=kx+a中，
则
，
解得：
，
故直线BC的解析式为：y=3x+6.
【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况，学校随机调查了本校50名学生参加社区活动的次数，并将调查所得的数据整理如下：
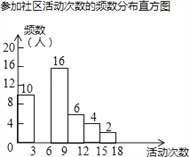
参加社区活动次数的频数、频率分布表
活动次数x | 频数 | 频率 |
0＜x≤3 | 10 | 0.20 |
3＜x≤6 | a | 0.24 |
6＜x≤9 | 16 | 0.32 |
9＜x≤12 | 6 | 0.12 |
12＜x≤15 | m | b |
15＜x≤18 | 2 | n |
根据以上图表信息，解答下列问题：
（1）表中a= ，b= ；
（2）请把频数分布直方图补充完整（画图后请标注相应的数据）；
（3）若该校共有1200名学生，请估计该校在上学期参加社区活动超过6次的学生有多少人？
【题目】随机抽取某理发店一周的营业额如下表（单位：元）：
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
540 | 680 | 760 | 640 | 960 | 2200 | 1780 | 7560 |
（1）求该店本周的日平均营业额.
（2）如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额，你认为是否合理？如果合理，请说明理由；如果不合理，请设计一个方案，并估计该店当月（按30天计算）的营业总额.
