题目内容
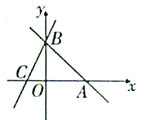
【题目】如图，在Rt△ABC中，∠C=90°，∠A=45°，AC=10cm，点D从点A出发沿AC方向以1cm/s的速度向点C匀速运动，同时点E从点B出发沿BA方向以
cm/s的速度向点A匀速运动，当其中一个点到达终点时，另一个点也随之停止运动，设点D，E运动的时间是t(0<1≤10)s．过点E作EF⊥BC于点F，连接DE，DE。
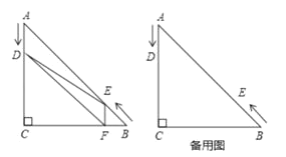
（1）用含t的式子填空：BE=________cm ，CD=________cm。
（2）试说明，无论t为何值，四边形ADEF都是平行四边形；
（3）当t为何值时，△DEF为直角三角形?请说明理由。
【答案】（1）（1）
t ，10-t；（2）见解析；（3）满足条件的t的值为5s或
s，理由见解析
【解析】
（1） 点D从点A出发沿AC方向以1cm/s的速度向点C匀速运动 ，由路程=时间×速度，得AD=t, CD=10-t,; 点E从点B出发沿BA方向以cm/s的速度向点A匀速运动,所以BE=t；
（2）因为 △ABC 是等腰直角三角形，得∠B=45°，结合BE= t，得EF=t,又因为∠EFB和∠C都是直角相等，得 AD∥EF，根据一组对边平行且相等的四边形是平行四边形，证得四边形ADFE是平行四边形；
（3） ①当∠DEF=90°时，因为DF平分对角，四边形EFCD是正方形，这时 AD=DE=CD=5，求得t=5;②当∠EDF=90°时，由DF∥AE，两直线平行，内错角相等，得∠AED=∠EDF=90°，结合∠A=45°，AD=AE , 据此列式求得t值即可； ③当∠EFD=90°，点D、E、F在一条直线上，△DFE不存在.
（1）由题意可得BE=tcm，CD=AC-AD=(10-t)cm，
故填：t ，10-t；
（2）解：如图2中
∵CA=CB，∠C=90°
∴∠A=∠B=45°，
∵EF⊥BC，
∴∠EFB=90°
∴∠FEB=∠B=45°
∴EF=BF
∵BE=t，
∴EF=BF=t
∴AD=EF
∵∠EFB=∠C=90°
∴AD∥EF，
∴四边形ADFE是平行四边形
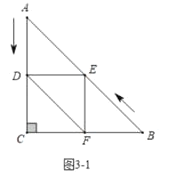
（3）解：①如图3-1中，当∠DEF=90°时，四边形EFCD是正方形，此时AD=DE=CD，
∴t=10-t,∴t=5
②如图3-2中，当∠EDF=90°时，
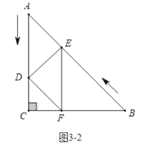
∵DF∥AC，
∴∠AED=∠EDF=90°，
∵∠A=45°
∴AD=AE，
∴t=(10- t)，
解得t=
③当∠EFD=90°，△DFE不存在
综上所述，满足条件的t的值为5s或s.
