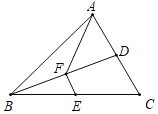
题目内容
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点![]() 匀速运动,当其中一点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一点到达终点时,另一个点也随之停止运动.设点![]() 、
、![]() 运动的时间是
运动的时间是![]() 秒
秒![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)四边形![]() 能够成为菱形吗?若能,求出
能够成为菱形吗?若能,求出![]() 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(3)当![]() ________时,
________时,![]() 为直角三角形.
为直角三角形.
【答案】(1)详见解析;(2)能;(3)2或![]() 秒
秒
【解析】
(1)在中![]() ,
,![]() ,
,![]() ,由已知条件求证;
,由已知条件求证;
(2)求得四边形![]() 为平行四边形,若使平行四边形
为平行四边形,若使平行四边形![]() 为菱形则需要满足的条件及求得;
为菱形则需要满足的条件及求得;
(3)分三种情况:①![]() 时,四边形
时,四边形![]() 为矩形.在直角三角形
为矩形.在直角三角形![]() 中求得
中求得![]() 即求得.②
即求得.②![]() 时,由(2)知
时,由(2)知![]() ,则得
,则得![]() ,求得
,求得![]() .③
.③![]() 时,此种情况不存在.
时,此种情况不存在.
(1)在![]() 中,
中,![]()
![]()
∴![]()
又∵![]()
∴![]()
(2)能. 理由如下:
∵![]() ,
,![]()
∴![]()
又∵![]()
∴四边形![]() 为平行四边形
为平行四边形
在![]() 中,
中,![]()
∴![]()
又∵![]()
∴![]()
∴![]() ,
,![]()
∴![]()
当![]() 时,
时,![]() 为菱形
为菱形
∴AD=![]()
∴![]() ,即
,即![]() 秒时,四边形
秒时,四边形![]() 为菱形
为菱形
(3)①![]() 时,四边形
时,四边形![]() 为矩形.
为矩形.
在![]() 中,
中,![]() ,
,
![]() .
.
即![]() ,
,![]() .
.
②![]() 时,由(2)四边形
时,由(2)四边形![]() 为平行四边形知
为平行四边形知![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
则有![]() ,
,![]() .
.
③当![]() 时,此种情况不存在.
时,此种情况不存在.
综上所述,当![]() 秒或
秒或![]() 秒时,
秒时,![]() 为直角三角形.
为直角三角形.

【题目】越来越多的人在用微信付款、转账,把微信账户里的钱转到银行卡叫做提现。
自2016年3月l日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000元的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为l600元,他需支付手续费_________元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下:
第1次 | 第2次 | 第3次 | |
提现金额(元) | A | b |
|
手续费(元) | 0 | 0.4 | 3.4 |
问:小明3次提现金额各是多少元?
(3)单笔手续费小于0.1元的,按照0.1元收取(即提现不足100元,按照100元收取手续费).小红至今共提现两次,每次提现金额都是整数,共支付手续费2.4元,第一次提现900元。求小红第二次提现金额的范围.
【题目】为选拔参加全市中学生数学竞赛的学生,八(2)班组织了一次班内数学竞赛活动,竞赛活动分小组进行,其中甲、乙两组各5人的成绩如下图所示(120分制).

(1)填写下表:
平均数 | 中位数 | |
甲 | ________ | 90 |
乙 | 90 | ________ |
(2)请计算甲、乙两组竞赛成绩的方差,并说明在这次数学竞赛中,哪一组的成绩更为稳定?